Unsupervised Learning - Dimensionality Reduction

Unsupervised Learning - Dimensionality Reduction#

img_p2_1

Unsupervised learning#

Statistical methods that extract meaning from data without training a model on labeled data

Unsupervised learning also constructs a model of the data but it doesn’t distinguish between target and predictor variables

  • finding groups of data → Clustering

  • reducing the dimensions of the data to a more manageable set of variables → Dimensionality Reduction

  • extension to EDA - when you have large number of variables and records

The curse of Dimensionality: Intuition#

To which category does x belong to?

Blue / Red / Green?

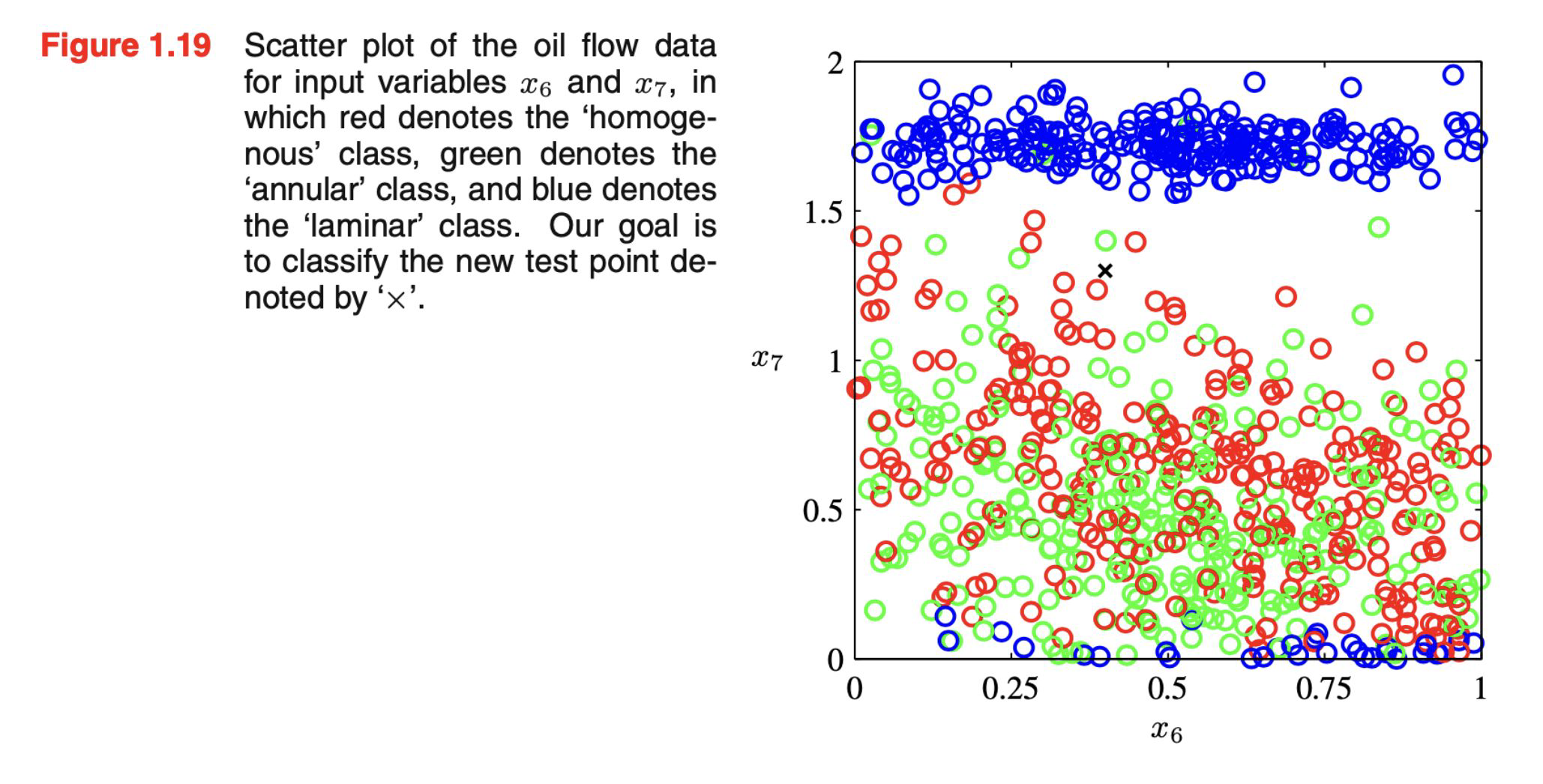
Intuition: The identity of x should be determined more strongly by nearby training points and less so by further away training points

Simple approach: Divide in cells x belongs to the majority class in it’s cell

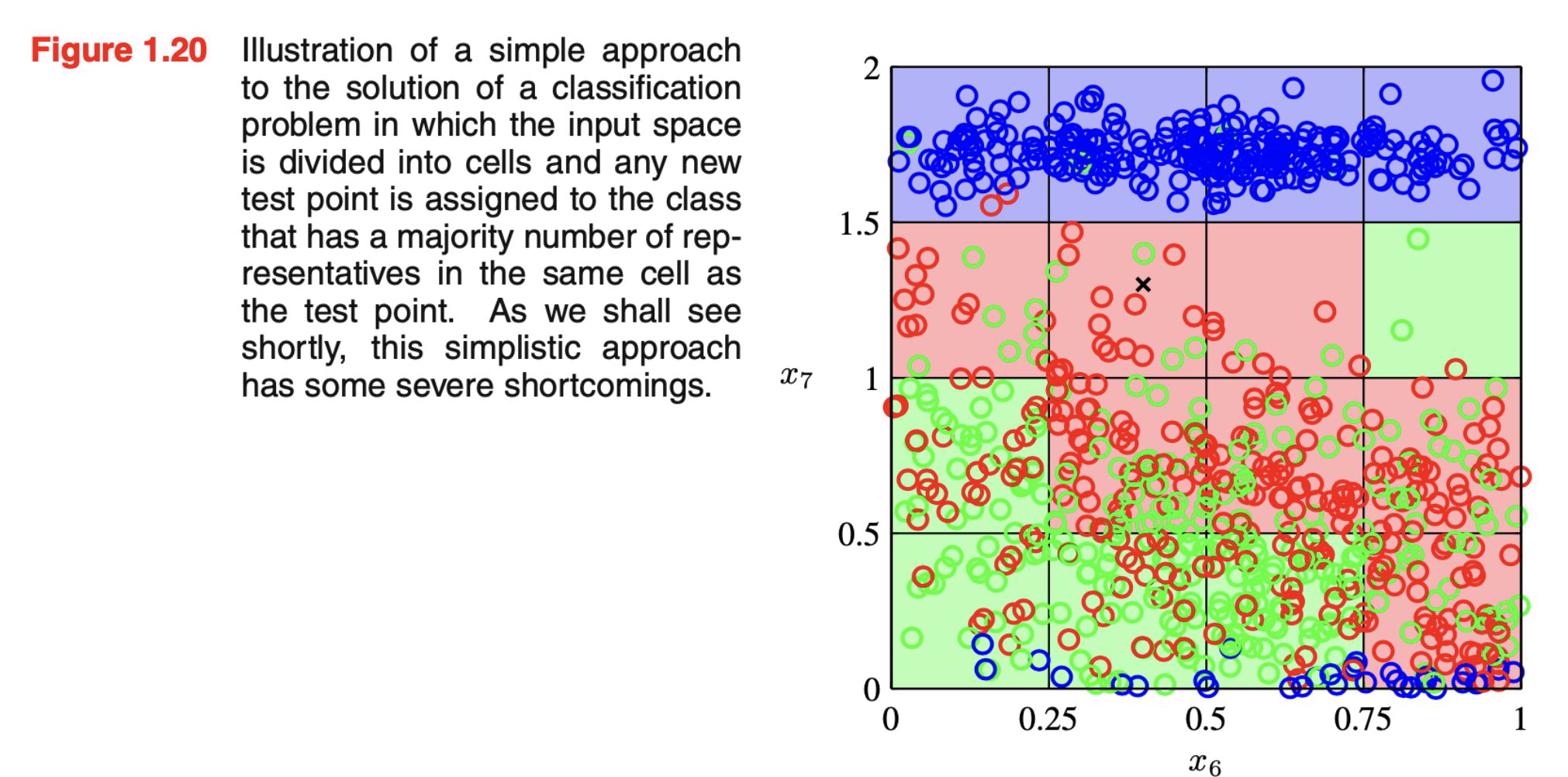
What if we have more dimensions?

The curse of Dimensionality: Intuition#

Do you think in all plots are the same amount of points?

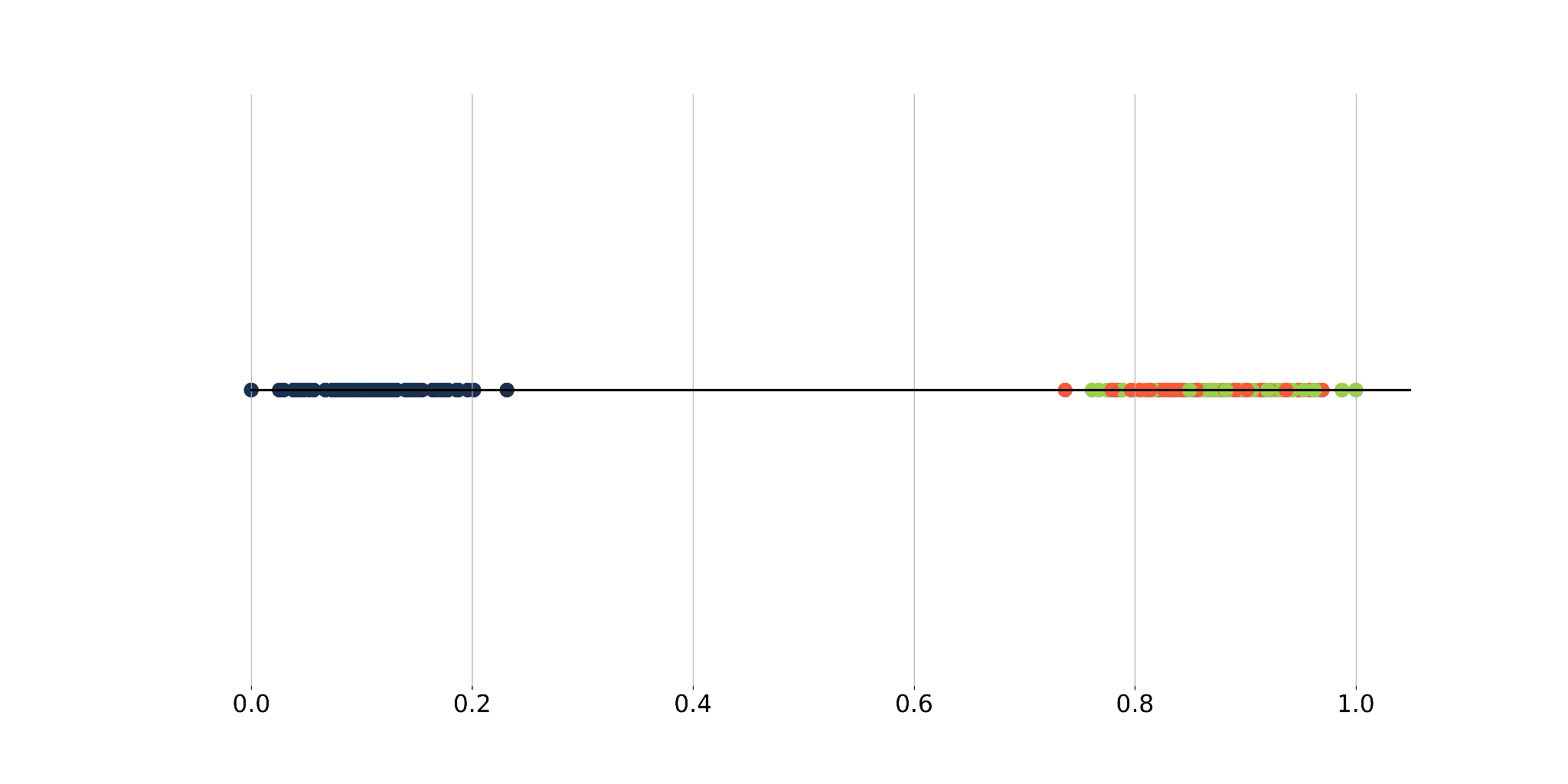
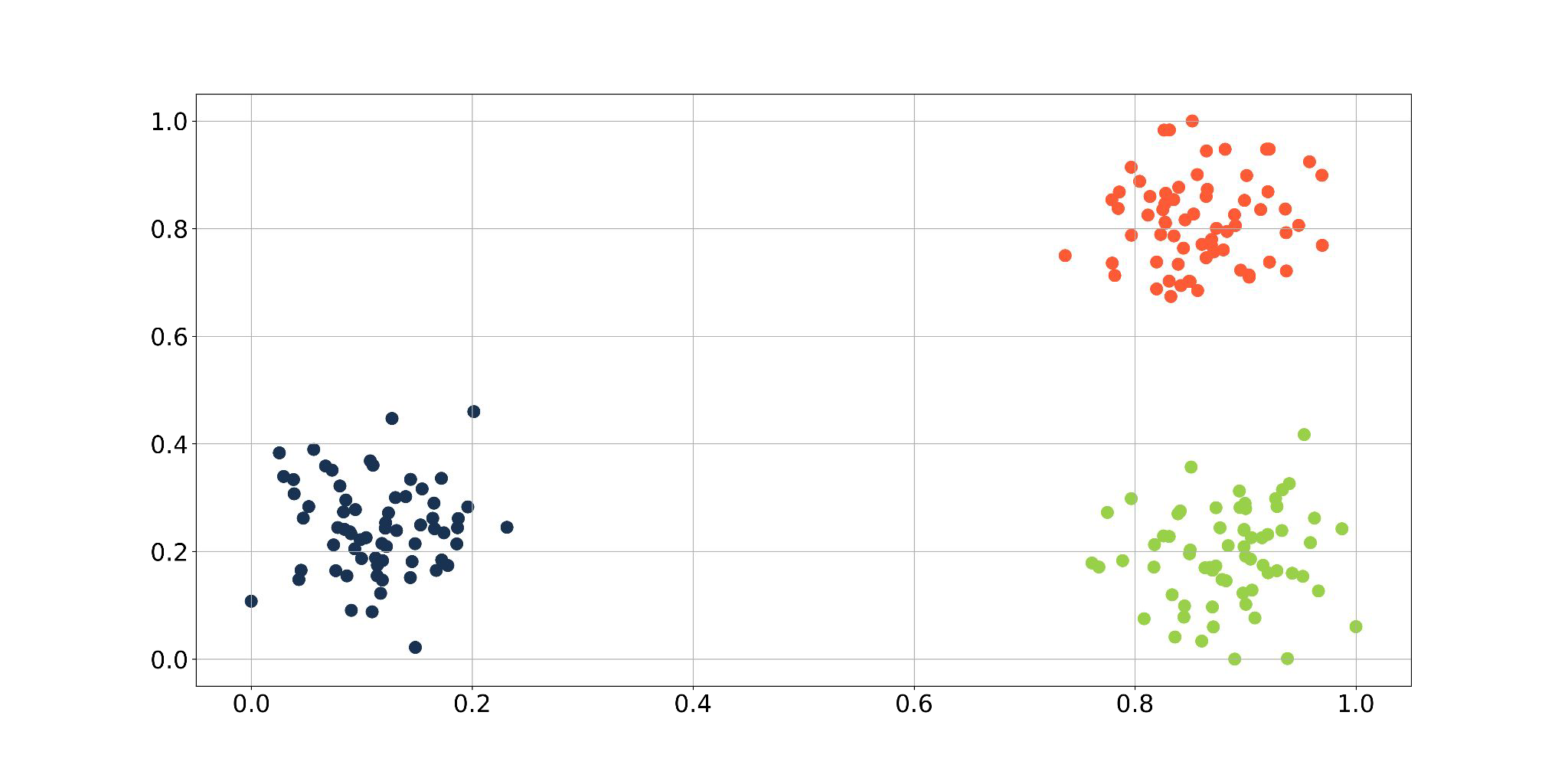
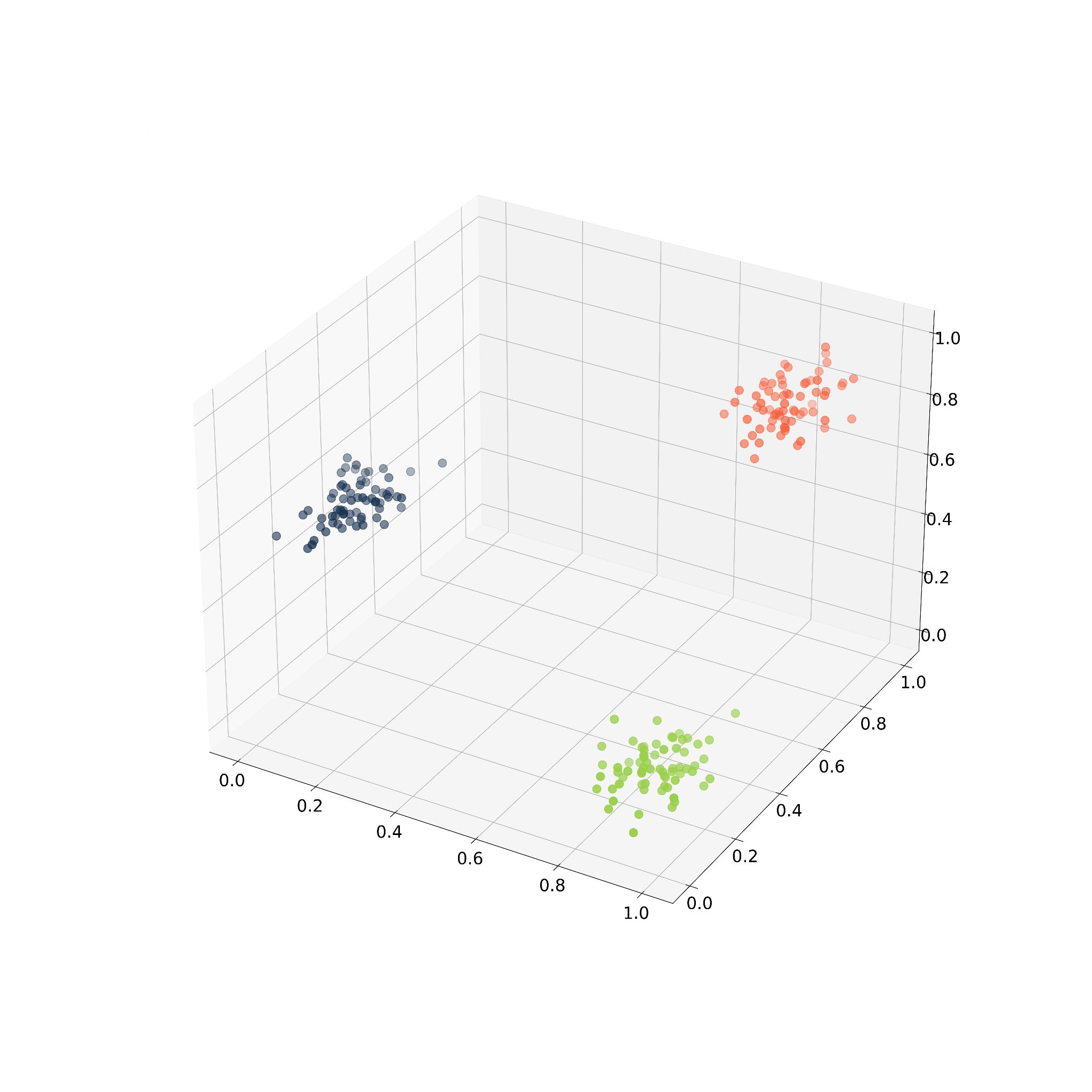
The curse of Dimensionality#

If we divide a region of a space into regular cells, the number of cells grows exponentially with the dimensionality of the space

Why is this a problem?

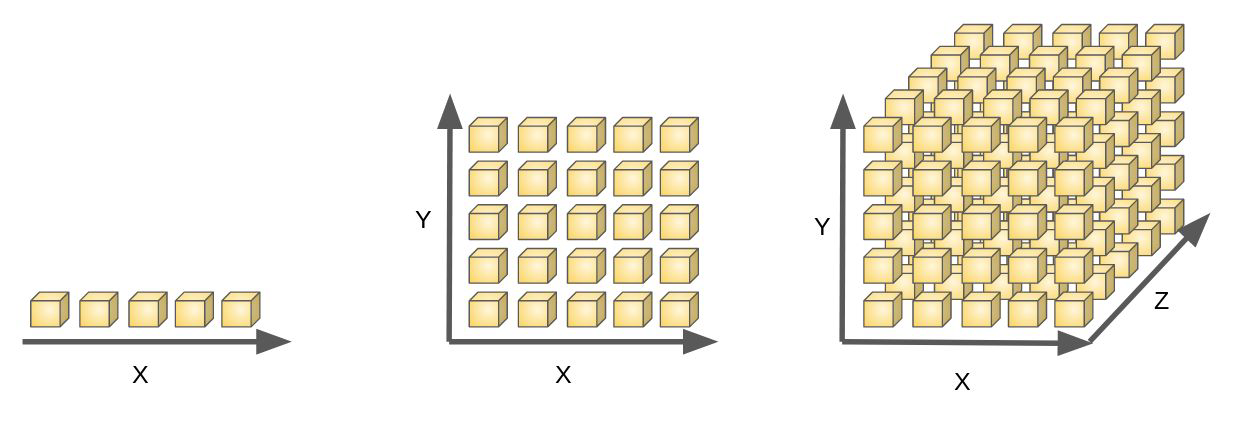
img_p10_1

How many data points do we need to cover all the cells?

We would need exponentially large quantity of training data to ensure all cells are filled

Note:

Sparse data: when you do not have data covering all cells!

I.e. between radius \(r_\text{i} = 1 - \epsilon \) (where \( \epsilon \) is the thickness of the shell) and \(r_\text{total}\) = 1 ?

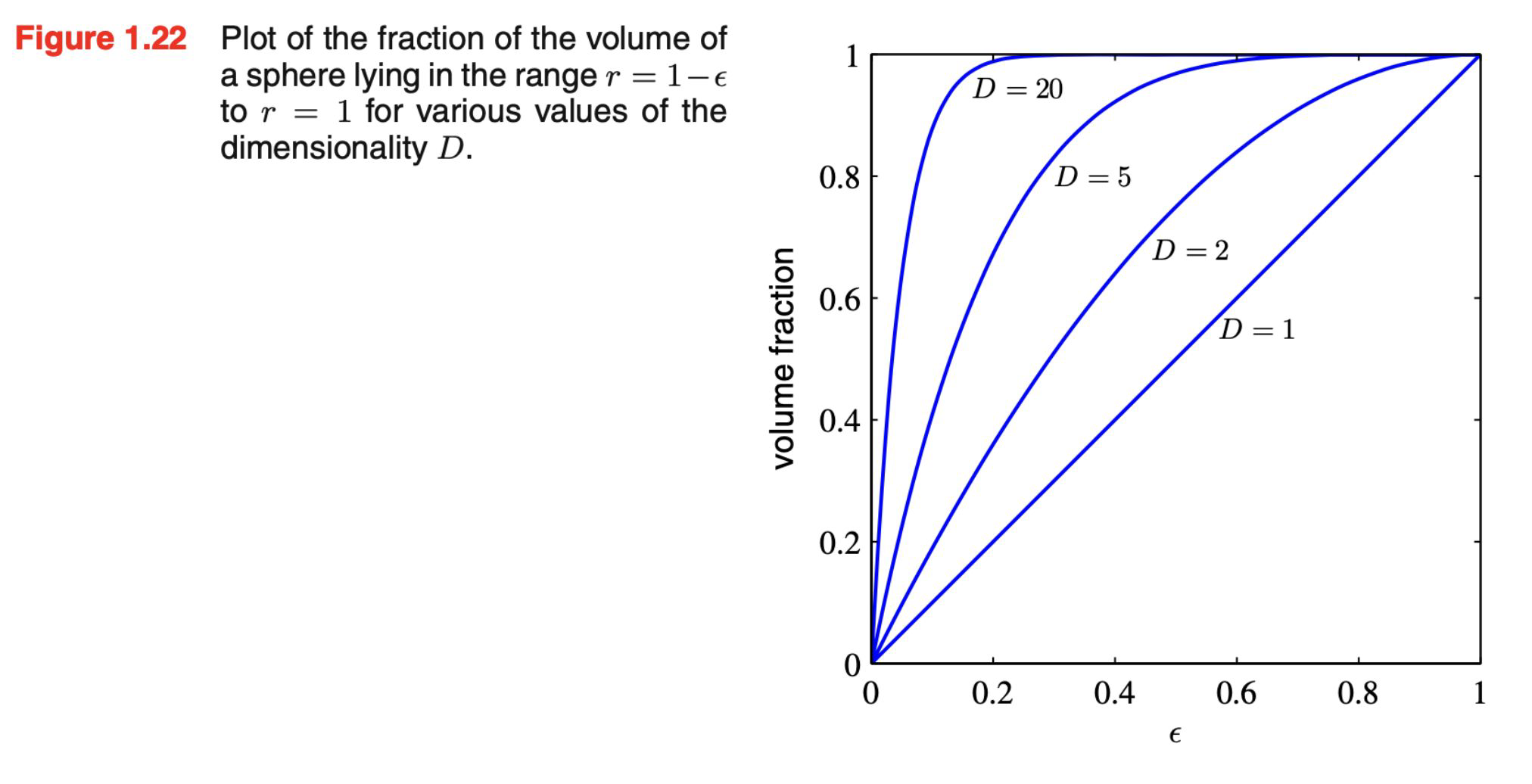
\[\begin{align} \frac{V_\text{Shell}}{V_\text{Total}} = \frac{V_\text{Total}-V_\text{Inner}}{V_\text{Total}} = \frac{1^D - (1 -\epsilon)^{D}}{1^{D}}= 1 - (1 -\epsilon)^{D} \end{align}\]

WHYYYYYYY!!????

The curse dimensions..#

we can still apply pattern recognition techniques to high-dimensionality data by exploiting these properties of real data:

  • may be confined to a region of the space having lower dimensionality, the directions over which important features may vary can be confined

  • will typically exhibit some smoothness properties and small changes in the input variables will produce small changes in the target variable

    • use local-interpolation techniques to make predictions for new values

The Manifold Hypothesis#

Real-world high-dimensional data lies on low-dimensional manifolds

  • manifolds are embedded within the high-dimensional space

  • manifolds are topological spaces that behave locally like Euclidean spaces

https://deepai.org/machine-learning-glossary-and-terms/manifold-hypothesis

Manifold Hypothesis - Intuition#

“Most real-world high-dimensional datasets lie close to a much lower-dimensional manifold”

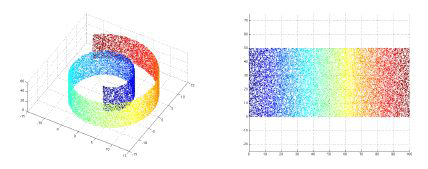
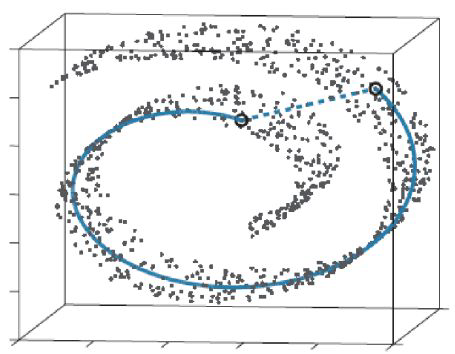
  • typical example: swiss roll

  • 2D plane, bent and twisted in 3rd dimension

  • one dimension: line, circle, but not an 8

  • two dimensions: surface, sphere, plane

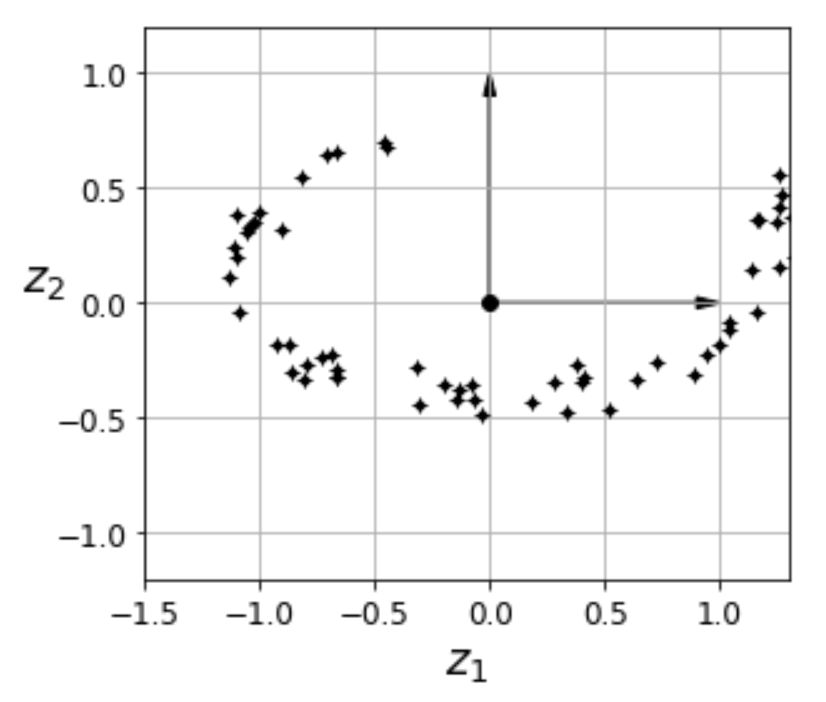
    • purpose is to unroll the swiss roll

    • the real euclidean distance between the two points is the solid line, not the dotted one

Getting the best point of view = maximizing the line of sight#

img_p18_0

Getting the best point of view = maximizing the line of sight#

img_p18_1

Advantages#

  • Speeds up subsequent algorithm

  • Data compression without substantial loss of information

  • Helps visualizing patterns

  • Can improve results through noise reduction (only sometimes)

Disadvantages#

  • Potential information loss

  • Computational cost

  • Transformed features may be hard to interpret

PCA#

Principal Component Analysis#

Goal is to reduce dimensions of feature space while preserving as much information as possible by:

➔ Finding new axis (= principal components) that represents the largest part of variance

  • principal components must be orthogonal (=independent) to each other

  • you can have just as many principal components as features

➔ keep only the most informative principal components

Principal Component Analysis#

PCA: combine the numeric predictors into a smaller set of variables, which are weighted linear combinations of the original set

  • the smaller set of variables, the principal components, explains most of the variability of the full set of variables

  • the weights reflect the relative contributions of the original variables

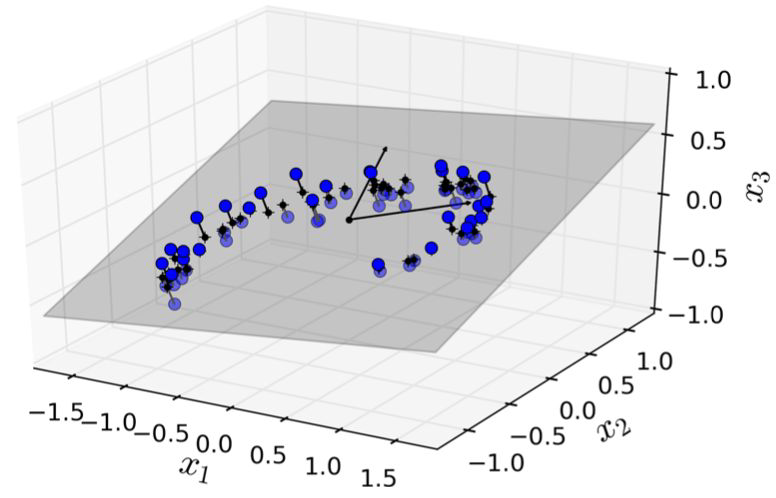
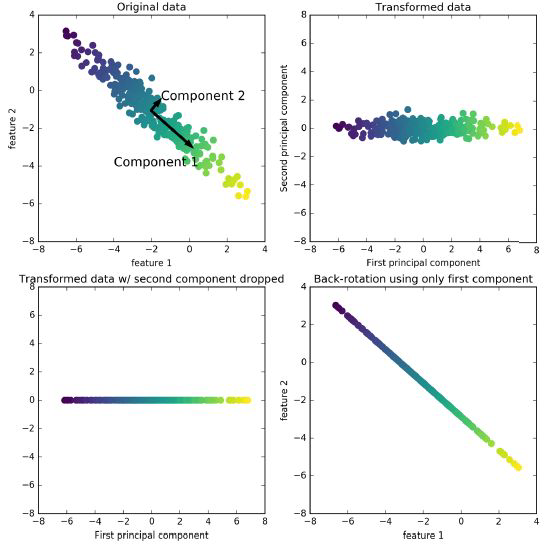
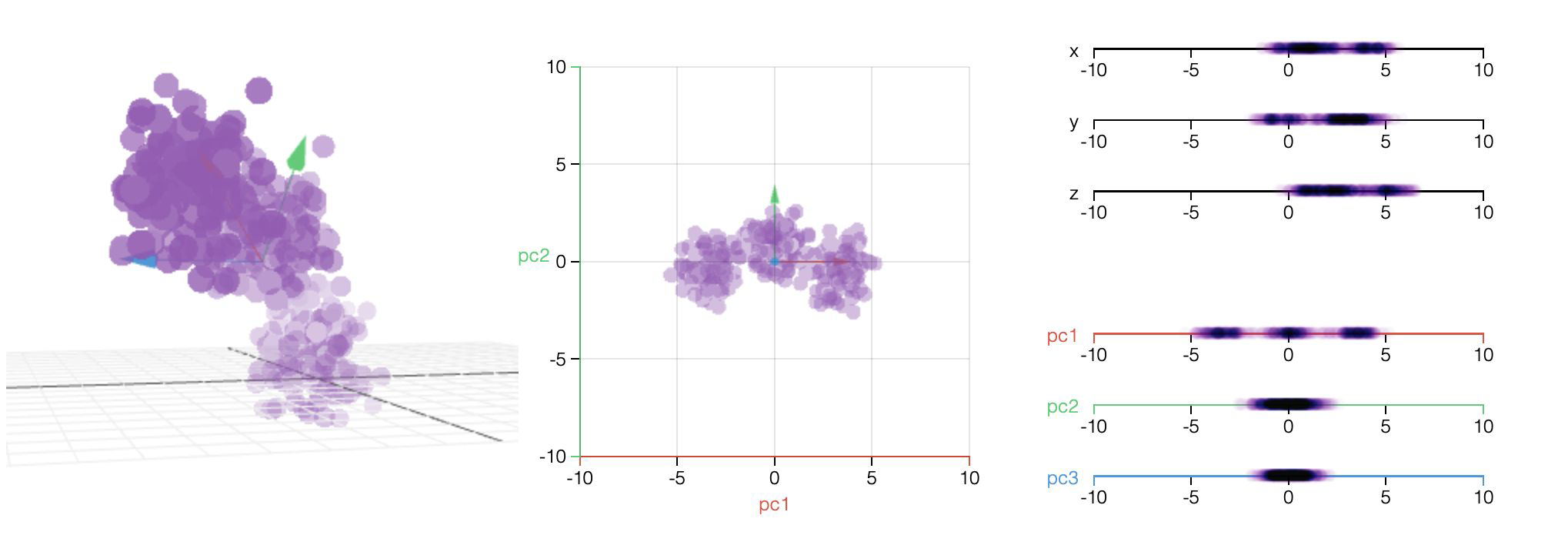
Principal Component Analysis - Projection to lower dimensions#

  • feature space (3D) reduced to lower dimensional subspace (2D)

  • the first 2 principal components can be presented as hyperplane

  • data is projected perpendicularly onto this hyperplane

Principal Component Analysis - Projection to lower dimensions#

Which line would you choose to preserve as much information as possible?

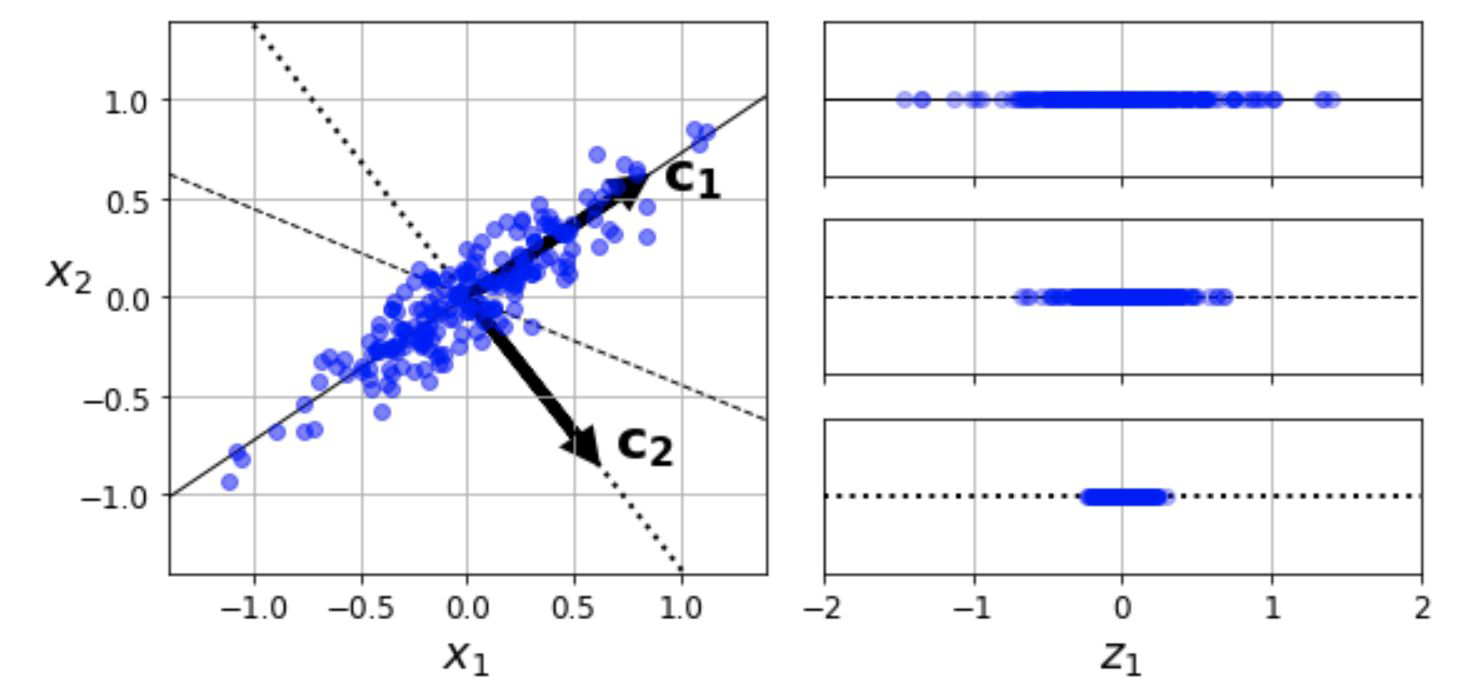
  • C1 preserves most of the variance

  • C2 (dotted line) is orthogonal to C1, preserves little variation

  • The unnamed, dashed line preserves an intermediate amount of variance

Principal Component Analysis - Transformation of Data#

  • important to transform data for PCA

  • centered around zero

  • principal components are combinations of features and can be presented in the original feature space

Principal Component Analysis#

Maximizing variance

https://setosa.io/ev/principal-component-analysis/

Principal Component Analysis - Explained Variance Ratio#

  • principal components are found by a standard matrix factorization technique (Singular Value Decomposition (SVD))

  • after identifying all PC, reduce the dimensionality of the dataset by keeping only the first d PC

    → look at the explained variance ratio of the PCs to decide how many d Dimensions to keep

    → take as many d PC that a sufficiently large portion of the variance is explained (eg 95%)

Principal Component Analysis for Compression#

Original Data (left picture)

  • 784 features

PCA

  • preserving 95% of variance

  • 154 PCs

  • only 20 % of original size!

Inverse Transformation (right picture)

  • transforms 154 PC back to 784 features

  • only slight quality loss

Principal Component Analysis - Eigen Faces#

Eigen Faces: using PCA as a compression algorithm for images

  • Each image is turned into a vector and PCA is used to get their principal components

  • Instead of the training images them selves, we use the linear combination of the PCs (here called Eigenfaces due to their apperance) to represent the images.

  • Before transformation:

    • 47 * 62 pixels (resolution) * 1000 (#Images) = 2.914.000 numbers,

  • After transformation using 12 Eigen-Faces:

    • 47 * 62 pixels (resolution) * 12 (#Used-Eigen-Faces) + 12 (#Used-Eigen-Faces) * 1000 (#Images) = 46.968 numbers

  • Each original image can be represented by a linear combination of 12 Eigen Faces. It will appear “blurry” -> but we also only need ~2% of the data to store them

img_p32_1

Notes: You can see that each eigen face is focusing on a different aspect of face recognition, e.g. some have black for the eyes, others for the nose bridge, or face shape (identify position). If a few of tehm already focus on the eyes, the other don’t need to because it was already well captured.

Principal Component Analysis - PC visualization#

  • with inverse transformation we can see what information is preserved after using different numbers of PCs

  • original picture: 2914 pixels

img_p33_1

Principal Component Analysis - Variants#

  • Randomized PCA: quick, approximation of first d components

  • Incremental PCA: for parallelization works with minibatches

  • Kernel PCA:

    • Kernel trick

    • complex nonlinear projections are possible

    • Preserves clusters of data after projection

    • can help to unroll data that lies on a manifold

PCA - Use Cases#

  • reduces the features space dimensionality.. it gets expensive to compute for more than few thousands of features

  • discards information from the data, downstream model may be cheaper to train, but less accurate

  • can be used in anomaly detection of time series

  • financial modeling - factor analysis

  • preprocessing step when learning from images -> may speed up the convergence of the algorithm

Other Techniques - linear#

  1. Linear Discriminant Analysis (LDA)

    → classification algorithm

    → finds discriminative axes that keep classes as far apart as possible

  2. Latent Semantic Analysis (LSA)

    → does not center the data before computing the singular value decomposition => can work with sparse matrices efficiently

    → also called truncated SVD

Other Techniques - non linear#

  1. t-Distributed Stochastic Neighbour Embedding (t-SNE) → based on probability distribution calculated with the distances between all points

  2. Uniform manifold approximation and projection (UMAP) → works with kNN (=> k is a hyperparamter also in UMAP) → faster than t-SNE

https://pair-code.github.io/understanding-umap/

References#

https://github.com/peteflorence/MachineLearning6.867/blob/master/Bishop/Bishop - Pattern Recognition and Machine Learning.pdf

https://en.wikipedia.org/wiki/Manifold https://www.researchgate.net/publication/2953663_Diagnosing_Network-Wide_Traffic_Anomalies

Feature Engineering for Machine Learning

Dogan (2013) Dogan, Tunca. (2013). Automatic Identification of Evolutionary and Sequence Relationships in Large Scale Protein Data Using Computational and Graph-theoretical Analyses.

A. Geron, ”Hands-on ML with scikit-learn and tensorFlow”, 2017

Kholodilin, Konstantin & Michelsen, Claus & Ulbricht, Dirk. (2018). Speculative price bubbles in urban housing markets: Empirical evidence from Germany. Empirical Economics. 55. 10.1007/s00181-017-1347-x. https://www.diw.de/documents/publikationen/73/diw_01.c.487920.de/dp1417.pdf

Müller, Andreas C., and Sarah Guido. Introduction to machine learning with Python: a guide for data scientists. “ O’Reilly Media, Inc.”, 2017.

https://www.geeksforgeeks.org/ml-face-recognition-using-eigenfaces-pca-algorithm/

Contents