Image Modeling

Image Modeling#

Warm-up đŸŒ¶ïž#

Spend some time looking at this explanation of Image Kernels (feel free to play around with all the settings!) and discuss the following questions:

  • What does the number at each pixel location in a greyscale image mean?

  • What is a kernel?

  • How is a kernel applied to an image?

  • How does changing the numbers in the kernel affect the output image?

  • What features of an image can we highlight using a kernel?

Motivation#

Image Data#

  • There is possibly no other data that has increased as much over the last decade - and filled our everyday life - as image data

  • In a single day on Instagram 1.3 billion photos and videos are uploaded (2023)

  • We want to process such data for many reasons

    • Image classification and captioning

    • Toxic content detection

    • Image quality improvements, etc.

Introduction#

How does image data look like?#

  • Image data has height, width and depth

    • Height and width are given in pixels

    • Depth is the number of channels (3 for RedGreenBlue, 1 for BlackWhite)

  • Each pixel corresponds to an integer between 0 and 255

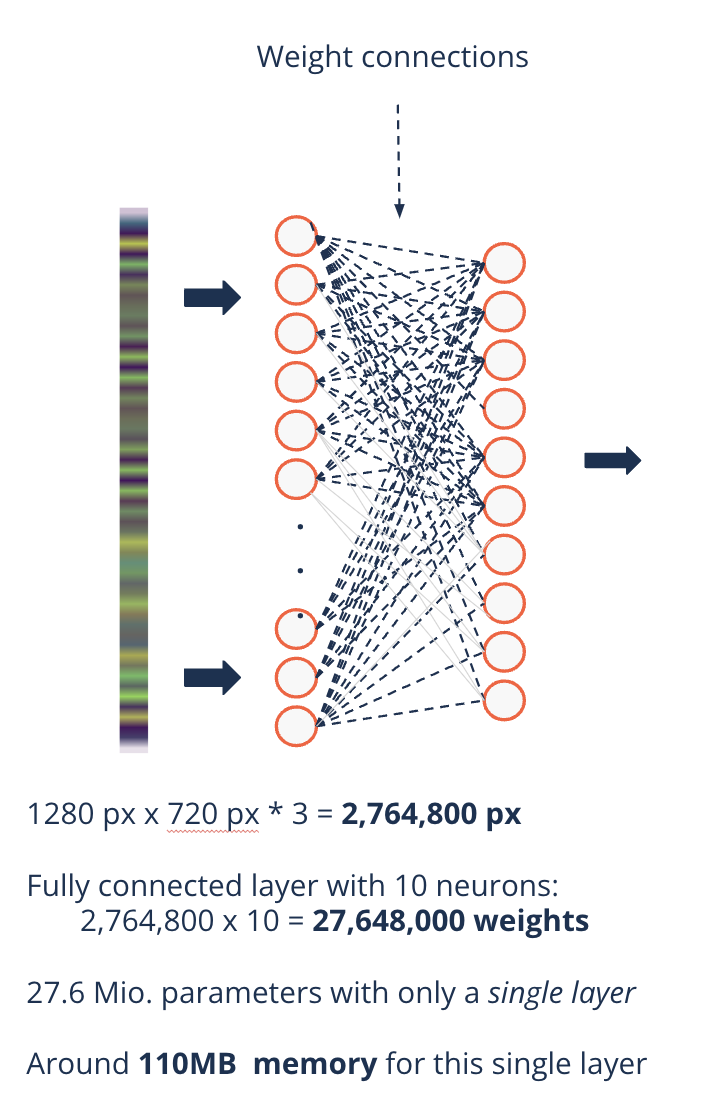
  • Example: A 1280 x 720 px color image has 1280 x 720 x 3 = 2,764,800 pixels = 2.76 MB

    • That is a lot to digest for an ML model using thousands of images for training and maybe hundreds in a batch

Unstructured data and locality#

  • In contrast to structured table data images show regularly transformations in local features

    • Different angles, rotations, flipping, scaling, translations

  • Humans can see the same objects just naturally

  • For an ML model this is a challenge

    • Transformation invariance is desired

Principle of locality#

  • Nearby pixels often show the same or a similar color

  • As pixels become further apart this similarity decreases or even breaks

  • Locality describes this phenomenon:

    • Locally pixels are correlated

Structured and unstructured data#

  • With structured data we would simply compare two feature vectors

    • Example: Structured truck data

Height (in m)

Weight (in m)

2.420

11

2.849

28

2.975

50

Source

Structured and unstructured data#

  • With structured data we would simply compare two feature vectors

    • Example: Structured truck data

Comparing the euclidean distance:

\((2.849-2.420)^{2}+(28-11)^{2}=289.19\)
\((2.975-2.420)^{2}+(50-11)^{2}=1,521.31\)

Height (in m)

Weight (in m)

2.420

11

2.849

28

2.975

50

Source

Structured and unstructured data#

  • With structured data we would simply compare two feature vectors

    • Example: Structured truck data

  • This does not work with image data comparing the vectors of all pixels (rolling them out)

    • The reason is locality (more generally transformation)

What is ideal feature information?#

  • The primary information to identify objects in an image are the pixel relations

    • Pixels distributed in a certain way identify a certain object

    • Colour compositions play in certain areas a crucial role

  • But how can we extract features that contain this information from an image?

    • This is a demanding task

  • How do we humans identify a fish as a fish?

Source

Image feature engineering#

  • Earlier approaches to image processing relied heavily on feature engineering by hand

    • Using edges to identify shape: edges are sharp changes in color

  • Some popular image features developed at these times

    • HOG (Histogram of Oriented Gradients) - Looking at changes in pixels

    • SIFT (Scale Invariant Feature Transform)

    • SURF (Speeded-Up Robust Feature)

The ideal feature information#

  • As an ideal, we want the model itself to find the best features to fulfill its task

  • How can a model map the high-dimensional image space to a lower dimensional subspace?

    • In which each image is represented by a long feature vector that behaves like structural data

  • In the following we try to find a model that can achieve this

Linear models for image modeling#

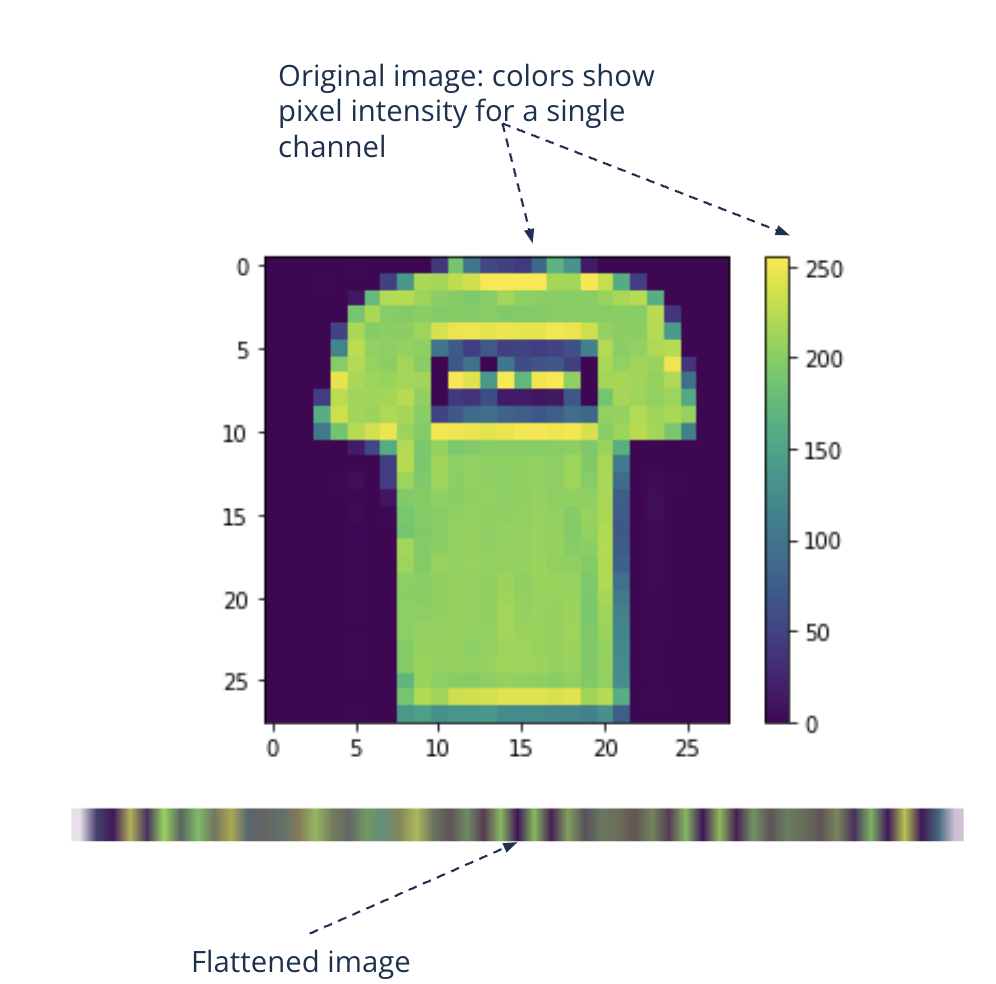
How to prepare the image data for a linear model?#

  • Given an image with height and width:

    • We could flatten the 2-dimensional tensor into a 1-dimensional one

    • Then just concatenating the channels therein

  • Given the label to be one of [T-shirt, Trouser, Pullover, Dress, Coat, Sandal, Shirt, Sneaker, Bag, Ankle boot]:

    • The label is represented by an integer between 0 and 9

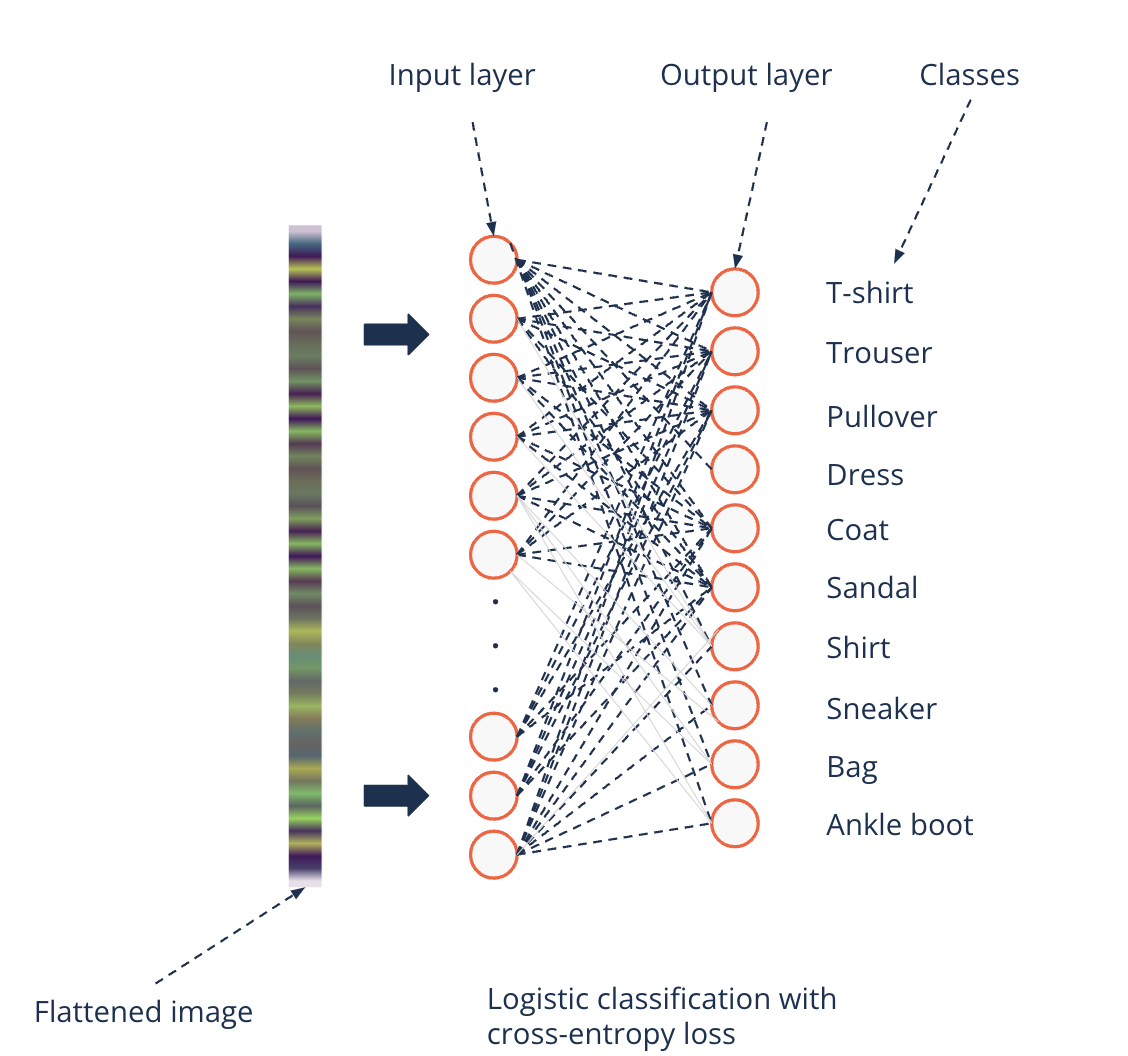
Logistic regression#

  • The logistic classification works on image data

    • On the MNIST Fashion dataset it reaches a 86% accuracy

    • That is almost a 15% error that could become costly in business

  • Can we improve modeling these image data?

Drawbacks of linear models#

  • Remember the TensorFlow playground

    • Linear models perform bad on non-linear data

    • Complex structures in data are hard to capture for linear boundaries

  • We need models capable of complex relationships between pixels

    • They must be able to approximate non-linear functions of high complexity

    • Such models must be able to do the feature engineering themselves

TensorFlow Playground

Deep Neural Networks for image modeling#

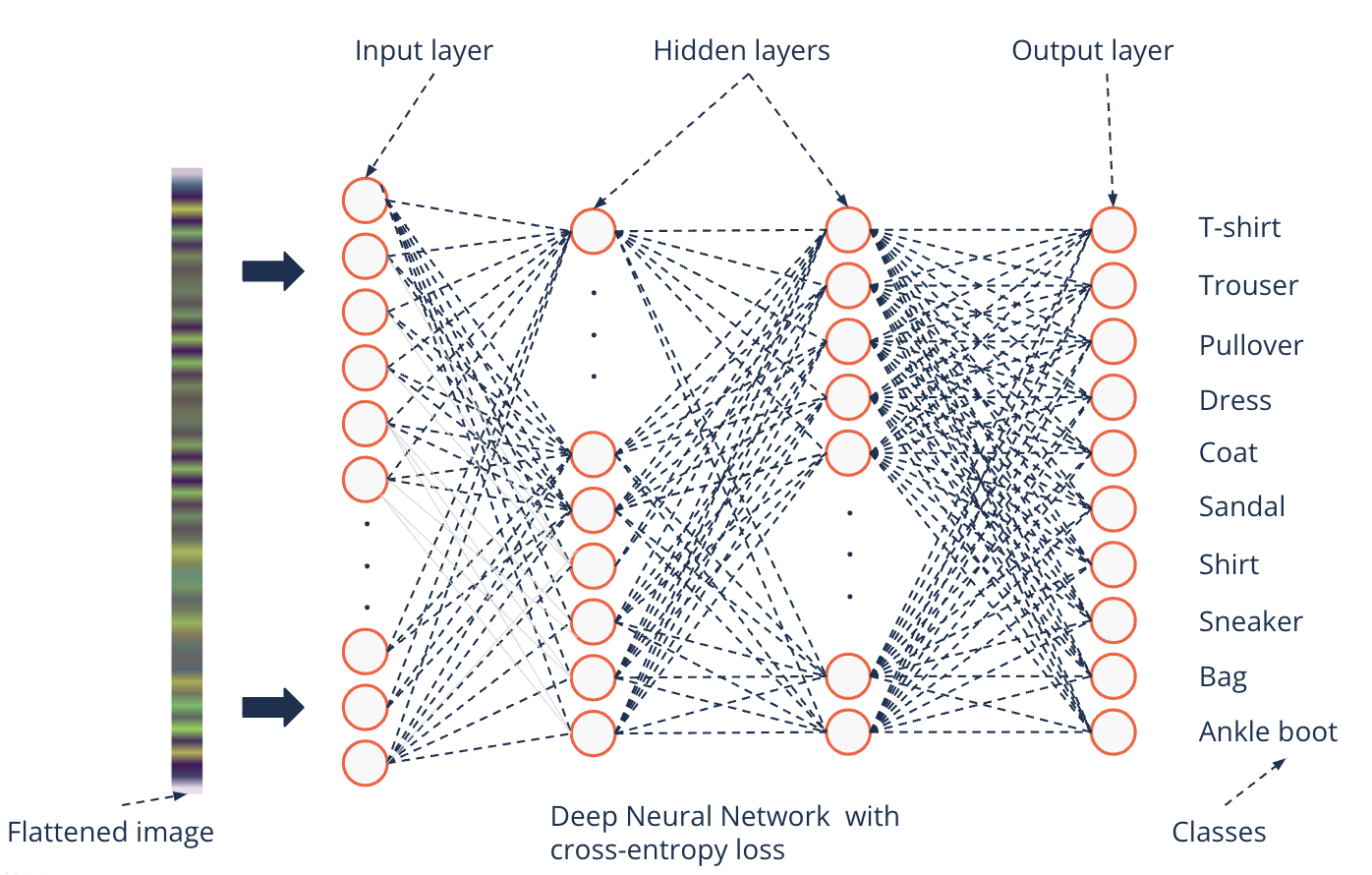
Deep Neural Networks perform better on image data#

  • Remember

    • Non-linear activation functions enable networks to model nonlinear functions

    • Hierarchy of neurons through layers make a complex feature extraction possible

  • Deep Neural Network on MNIST Fashion gets to a 91% accuracy

Drawbacks of Deep Neural Networks in image modeling#

  • Theoretically we can build a very deep network and approximate any function to classify images (universal approximation theorem), but

    • Very deep networks have high risk of overfitting

    • Real-world images have way more pixels

    • DNNs are not transformation invariant but are not dependent on the order of pixels either

      • i.e. the relationship between pixels does not count

ImageNet Competition#

  • ImageNet is the largest image recognition competition

    • ~1.2M images and 1,000 categories

  • Until 2011 feature engineering defined a dominant part for winning teams

    • Xerox XRCE team won by using Fisher Vectors (multi-dimensional SWIFT) and SVMs

  • 2012 AlexNet improved significantly and presented an implicit feature extraction

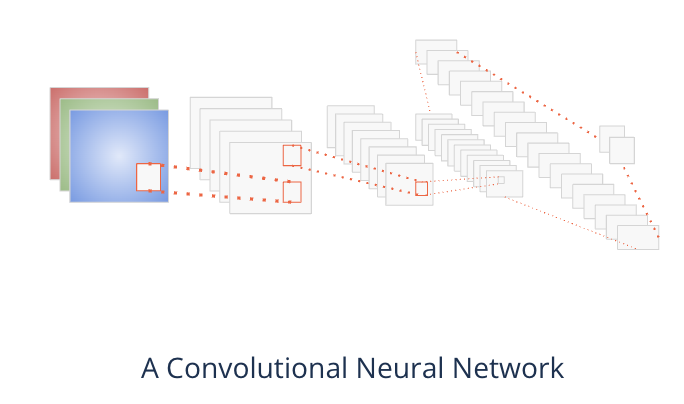
    • The authors used a {convolutional neural network (CNN)}

Convolutional layers#

Introduction#

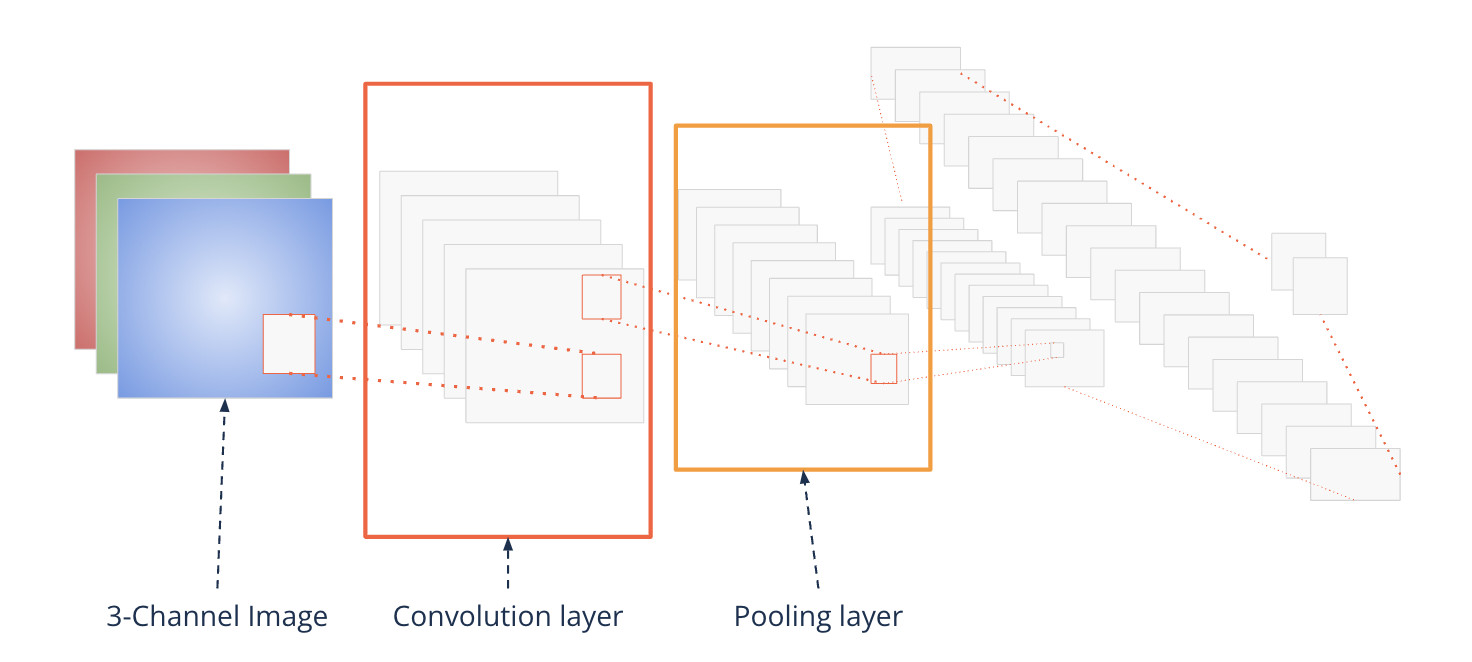
  • A convolutional neural network consists of two special layers:

    • Convolutional layers

    • Pooling layers

  • In the following we will consider these layers in detail

Convolution as a grouping of information#

  • We found out that the local relationships between pixels in an image contain important information

    • How can this relationship be captured?

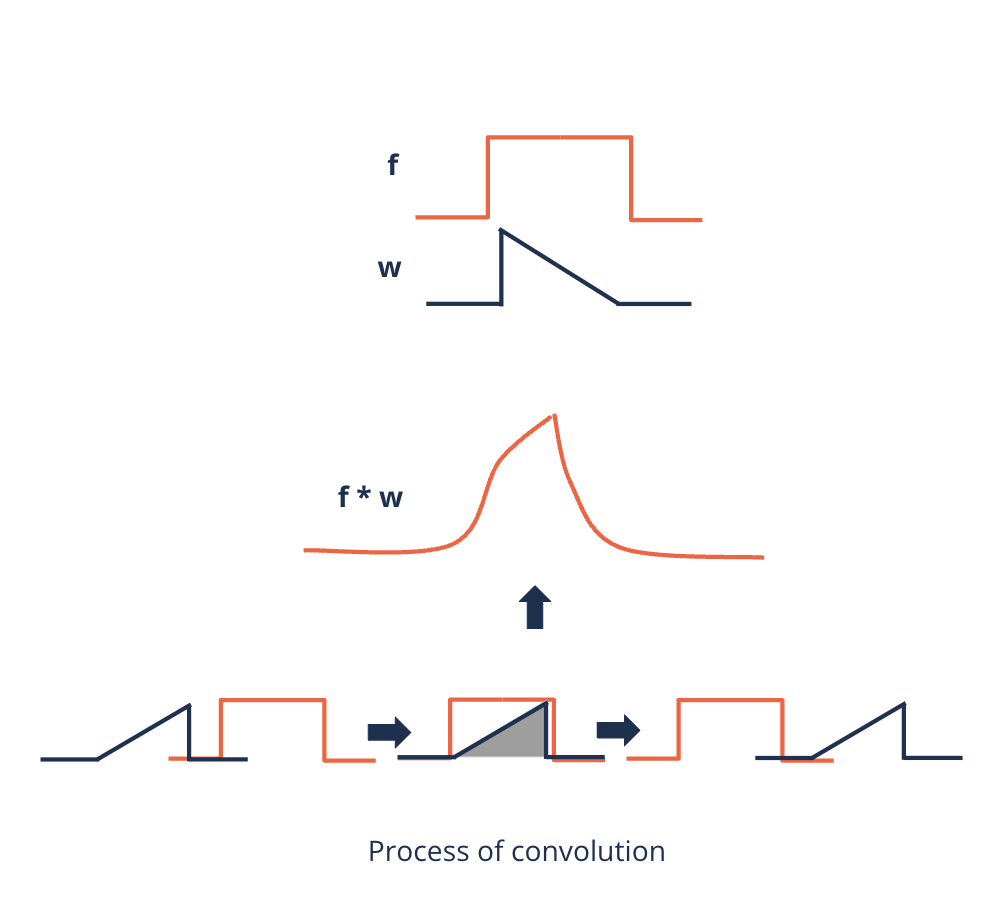
  • Convolutional layers use a special mathematical method to capture these relationships: a {convolution}

    • Intuitively, they take snapshots from all regions of an image and apply filters to them

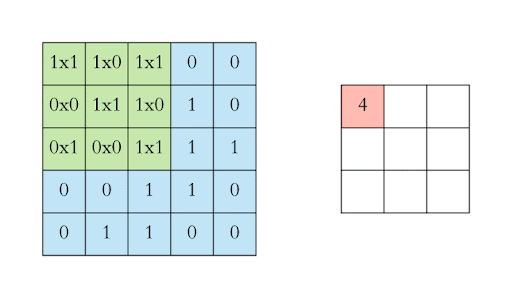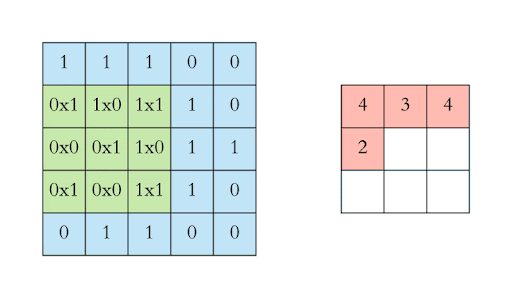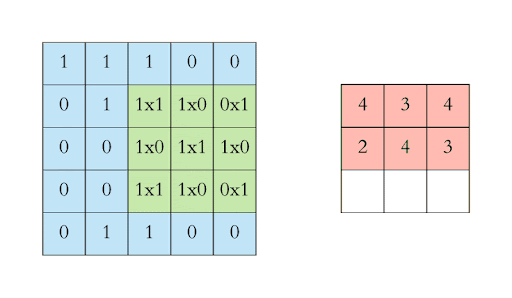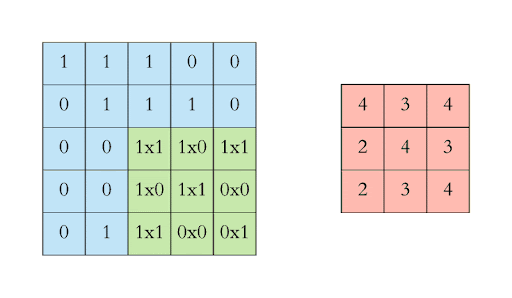
How does a convolution layer work?#


\[ y_{i,j}=\sum_{k}\,\sum_{l}\,w_{k l}\,x_{i+k,j+l}\]

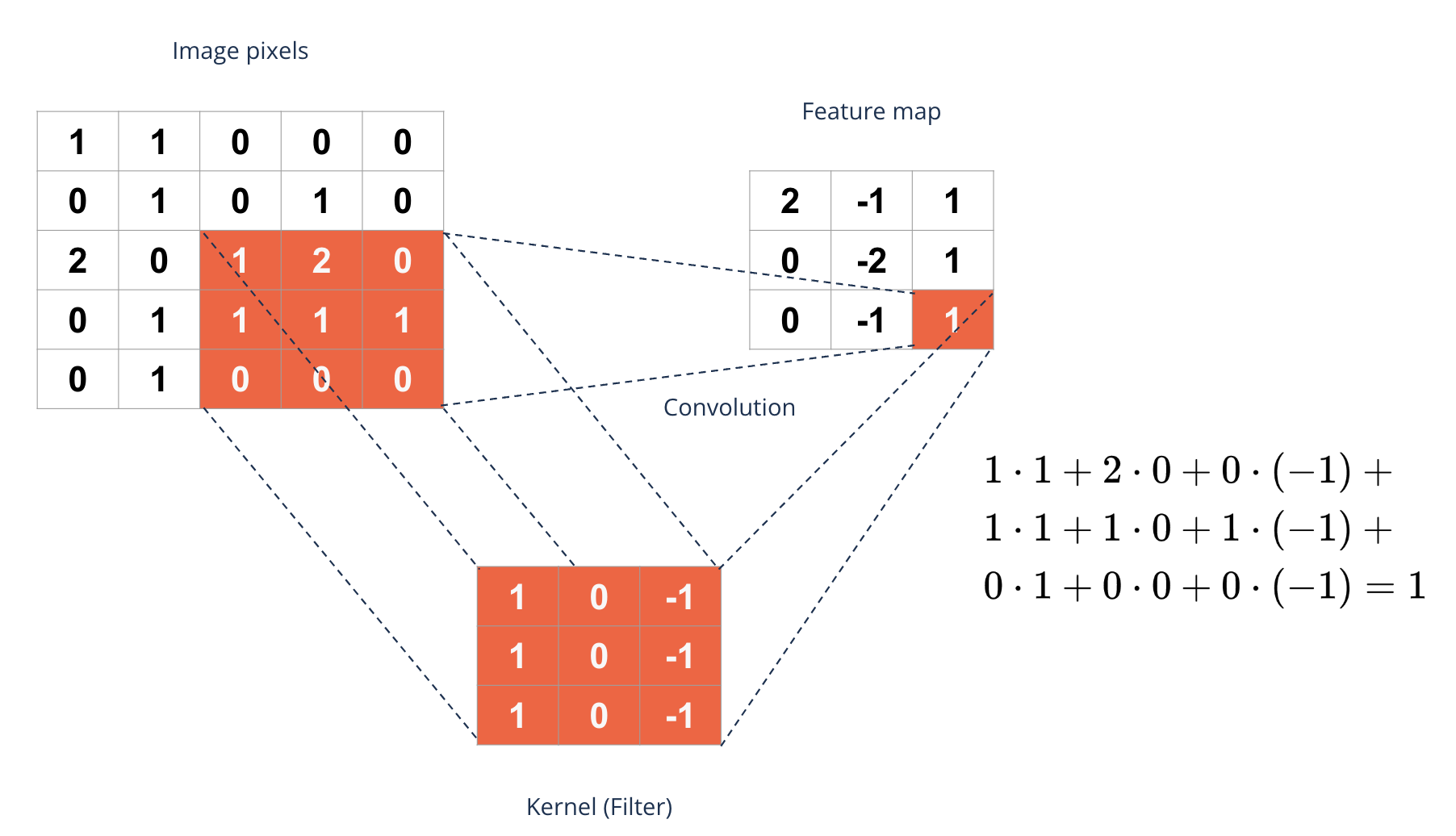
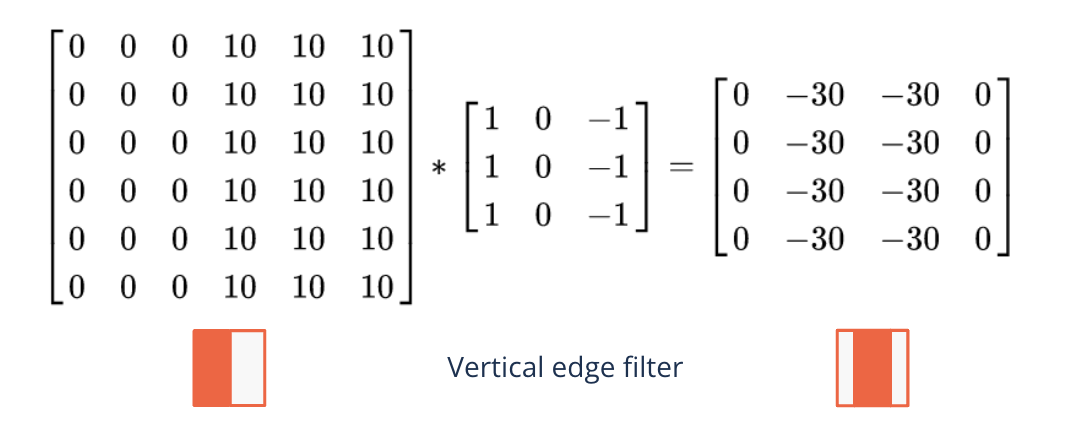
Edge detection#

  • A filter can detect different features in an image

    • Edges

    • Sharpening (edge detection + original image)

    • Blurring

  • Here we only look at edge detection to get an intuition how filtering works

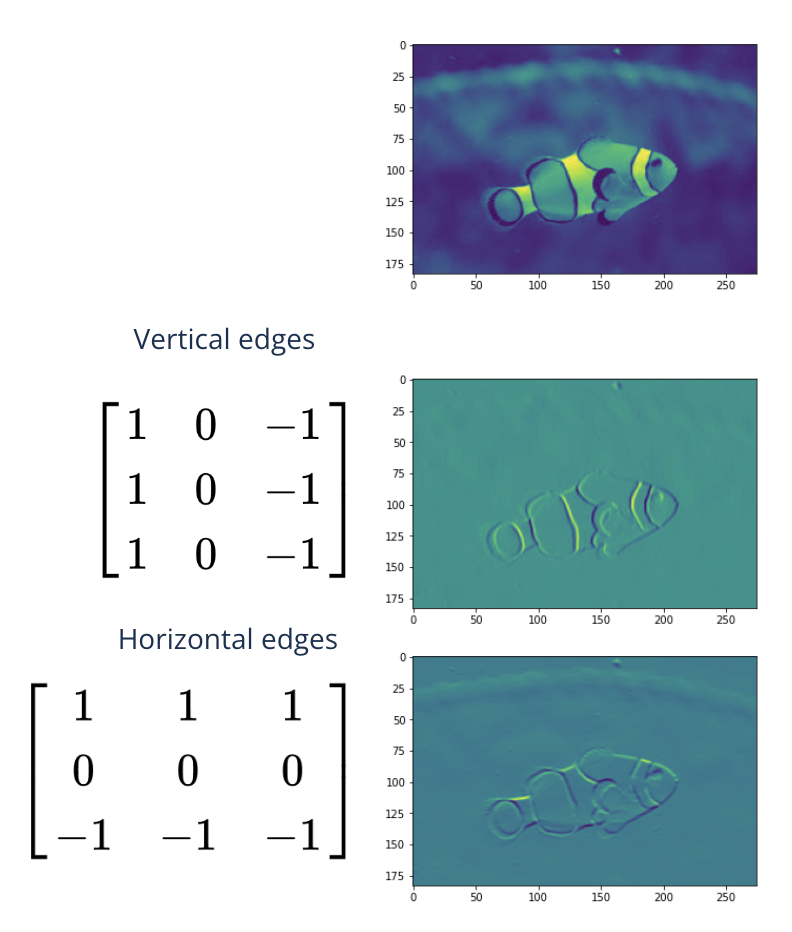
Major idea of a convolutional layer#

  • Filters can be constructed by hand

    • Why not learning filter values {parameters} in training?

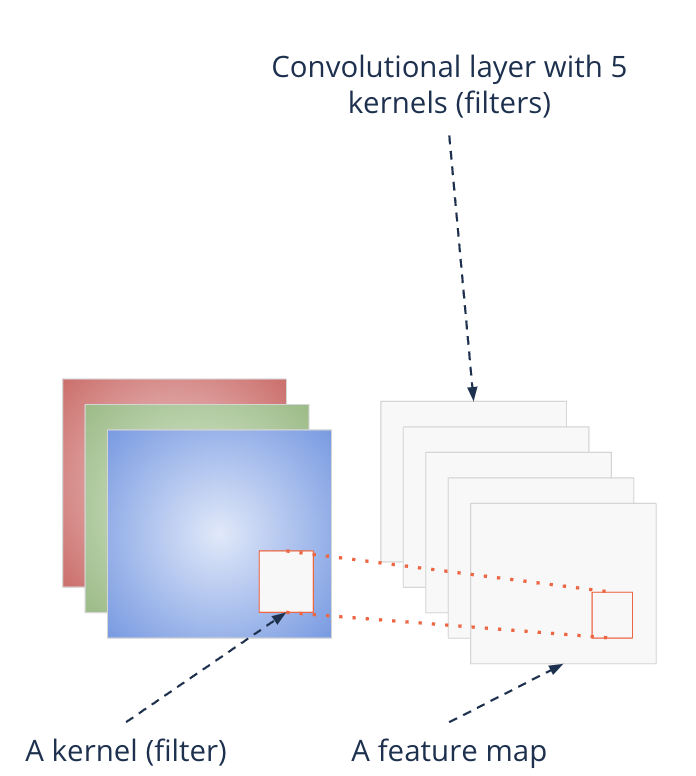
  • A convolutional layer contains many filters

    • Each filter forms during training

  • Each filter is of the same size and can process groups of nearby pixels

    • It looks at relationships between pixels {locality}

Reduction of dimensions#

  • Convolutional layers reduce the dimension of the image

    • A 28 x 28 picture filtered by a 3 x 3 kernel shrinks to a dimension of 26 x 26

  • This limits the number of convolutional layers applied to an image

    • At each layer the image shrinks

  • Formula for the resulting image dimension:

\[m=n-k+1\]
\[28-3+1=26\]

Source

How can we build deep convolutional networks?#

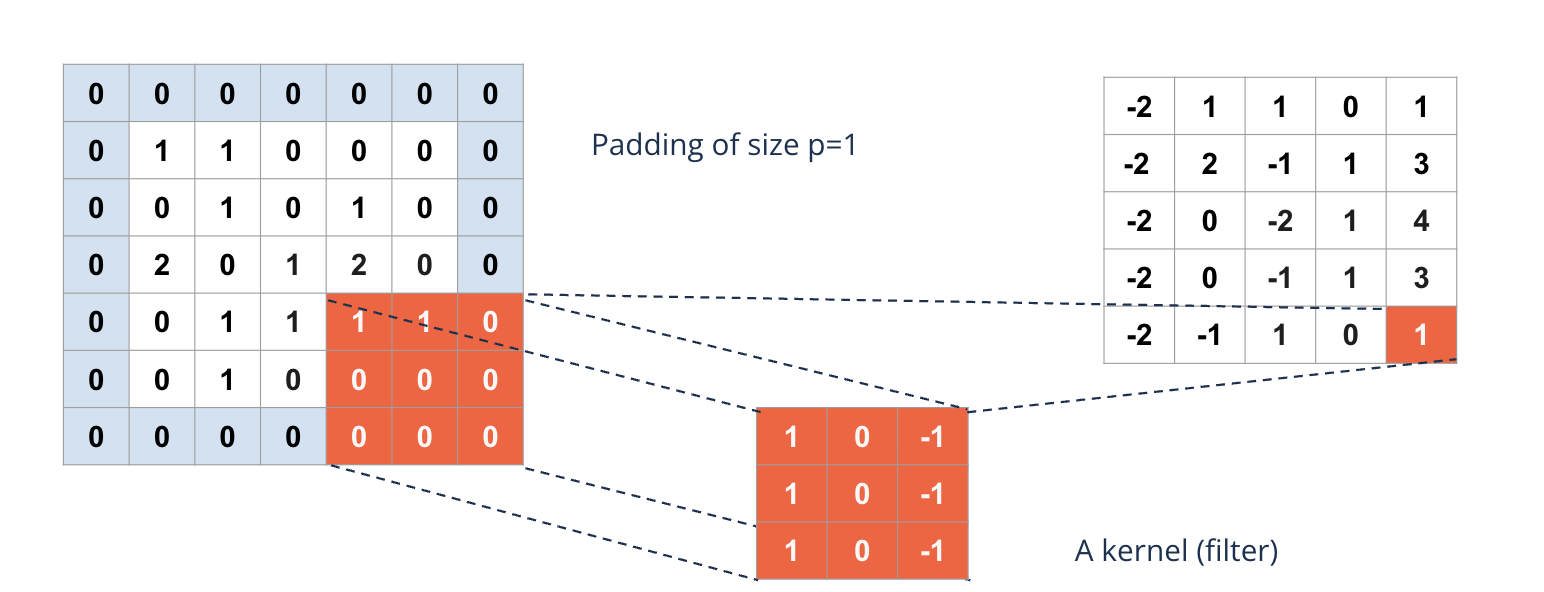
  • To avoid shrinking the image too quickly {padding} is applied

  • The image is ‘framed’ by zeros

    • A 28 x 28 image with a padding of 1 has dimension 30 x 30

    • WIth a kernel of 3 x 3 this results again in a 28 x 28 image

  • Formula for the resulting image size

\[m=n+2p-k+1\]
\[28+2*1-3+1=28\]

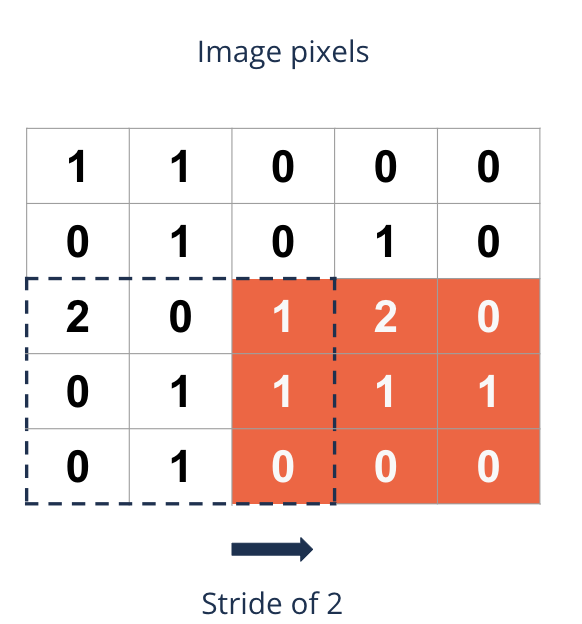
Making great strides#

  • Stride is the step size of the filter {kernel} by which it moves along the image

  • Sometimes a larger stride is desired

    • It reduces large image sizes to optimize memory usage and reduces computational costs

    • It reduces the risk of overfitting

  • Formula for the resulting image dimension (stride of 2):

\[m=\big\lfloor{\frac{n+2p-k}{s}}+1\big\rfloor\]
\[m=\big\lfloor{\frac{28+2\cdot0-3}{2}}+1\big\rfloor=13\]

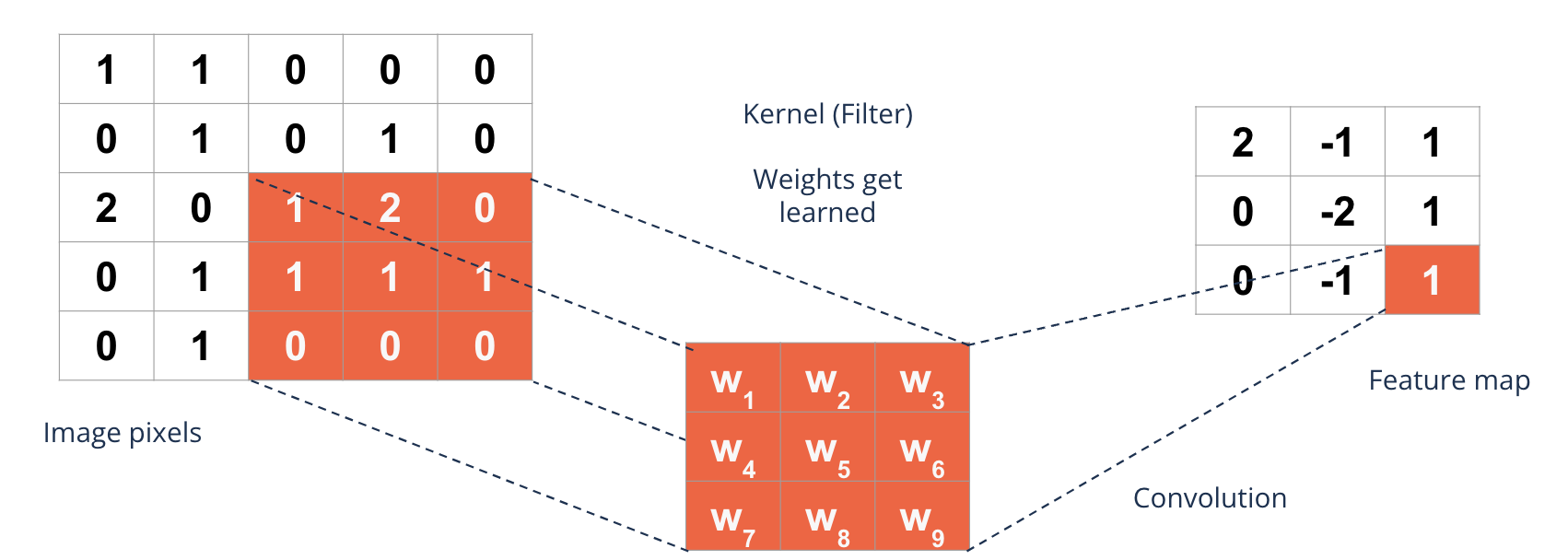
What happens during training?#

  • The filters {kernels} of a convolutional layer are variable

    • They get learned during training of the network

  • The network learns thereby optimal filters to fulfill its task

Stationarity principle#

  • There are features in an image that are essential and repeat themselves at different locations

  • Statistical signals are uniformly distributed:

    • These features have therefore also be detected at each location

  • This justifies {parameter sharing} which makes CNNs very parameter-efficient

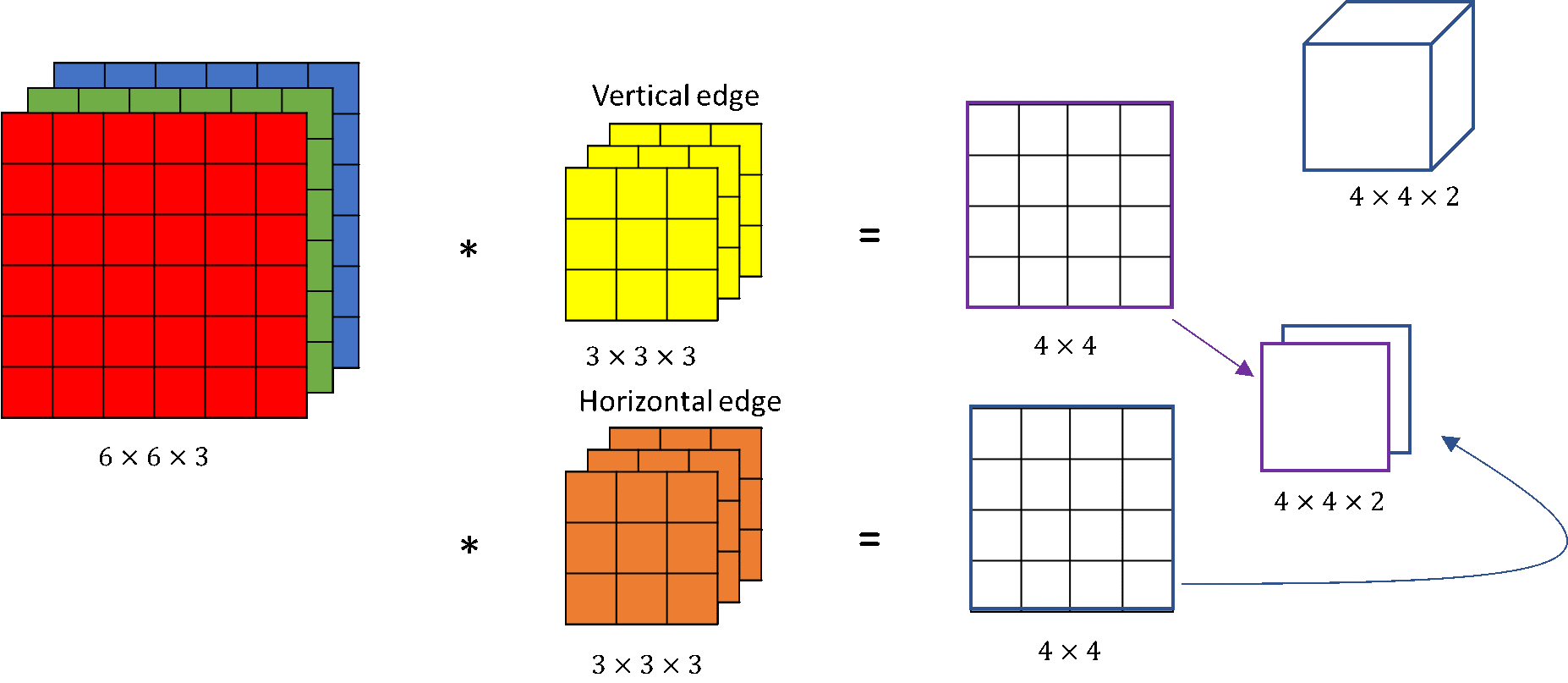
Working through the channels#

  • Color images have three channels

    • Convolutions take place across channels

    • I.e. a filter {kernel} is actually a cube

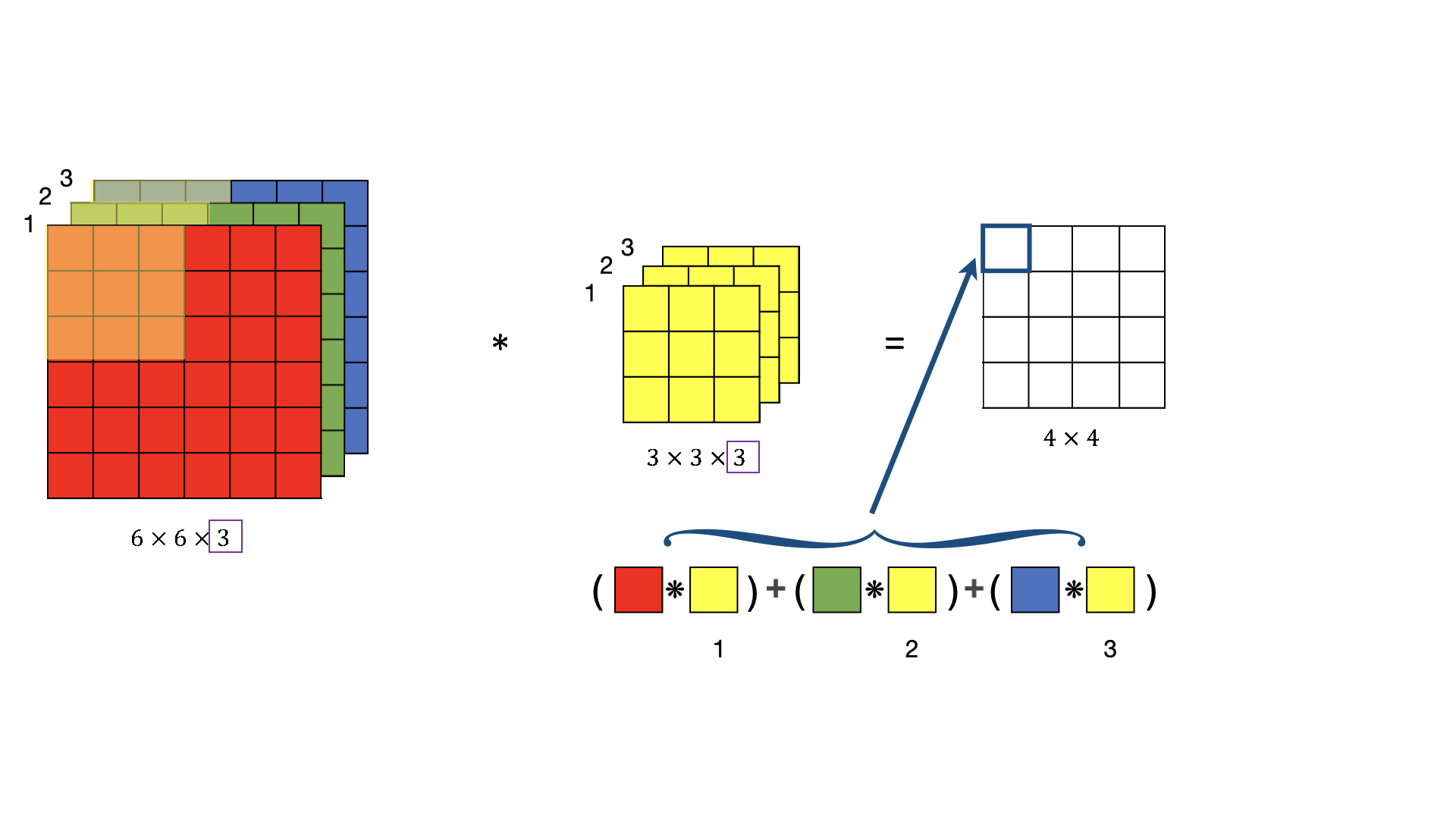
Working through the channels#

  • Color images have three channels

    • Convolutions take place across channels

    • I.e. a filter {kernel} is actually a cube

  • Per convolutional layer there are usually many filters applied

    • A filter per feature

    • I.e. the output is actually again multi-channel

    • The channel of the output is also called {feature map}

Parameter sharing is caring#

  • Remember the large image example (1280px x 720px):

    • 27.6 Mio. parameters with 10 neurons in a DNN

    • 110 MB in memory

  • Consider instead a convolutional layer with 64 filters of size 3x3 applied to a colour image

    • 3x3x3x64 + 64= 1792 parameters!

    • 7 KiB in memory

  • With parameter sharing we can train

    • faster

    • deeper networks

Pooling layers#

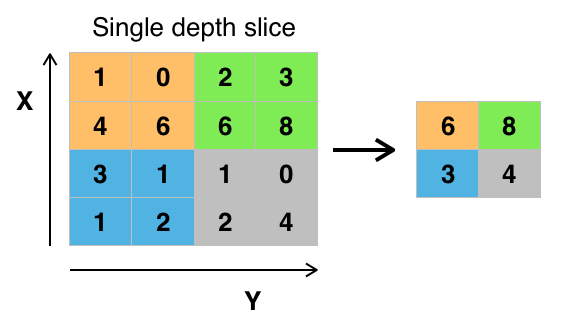
What is pooling?#

  • Pooling is aggregating features from {feature maps}

    • We pool over a certain window: we apply a summary of nearby pixels

    • The window is then moved across a feature map

  • Pooling reduces a feature map in size:

    • A 26 x 26 feature map with a 2x2 pooling layer reduces the feature map to dimension 25x25

  • Formula for the resulting dimension:

\[m=\big\lfloor{\frac{n+2p-k}{s}}+1\big\rfloor\]
\[m=\big\lfloor{\frac{26+2\cdot0-2}{1}}+1\big\rfloor=25\]

In practice pooling layers often use a stride corresponding to the kernel size: 2x2 kernel with stride of 2

How does a Pooling layer work?#

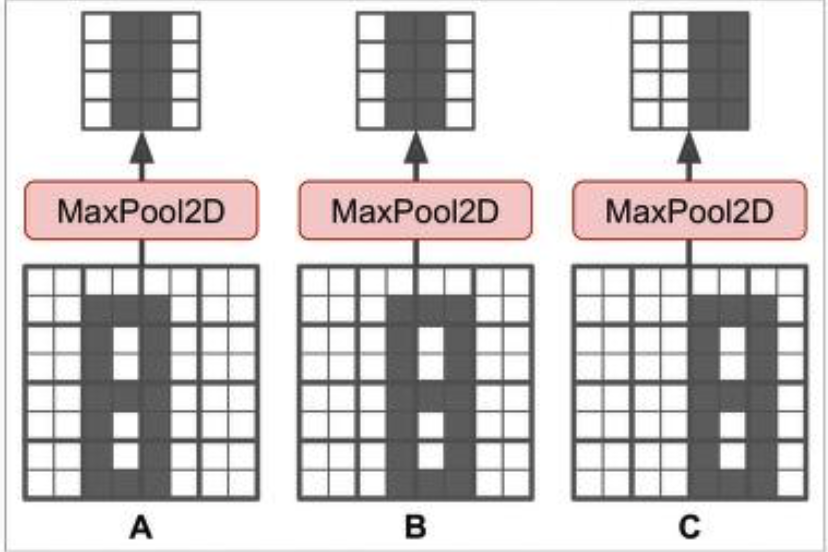
Why pooling?#

Pooling has two major effects:

  • It makes the network invariant to translations

source

Why pooling?#

Pooling has two major effects:

  • It makes the network invariant to translations

  • It strengthens the signal while it is running through the network

Compositionality principle#

  • Any image is compositional:

    • Features compose the image in a hierarchical manner

  • This justifies the use of multiple layers

    • Each layer composes features of the prior layer to a more complex one

Building the network#

  • Stack layers together with a softmax or sigmoid layer at the end

  • Train with gradient descent to optimize parameters

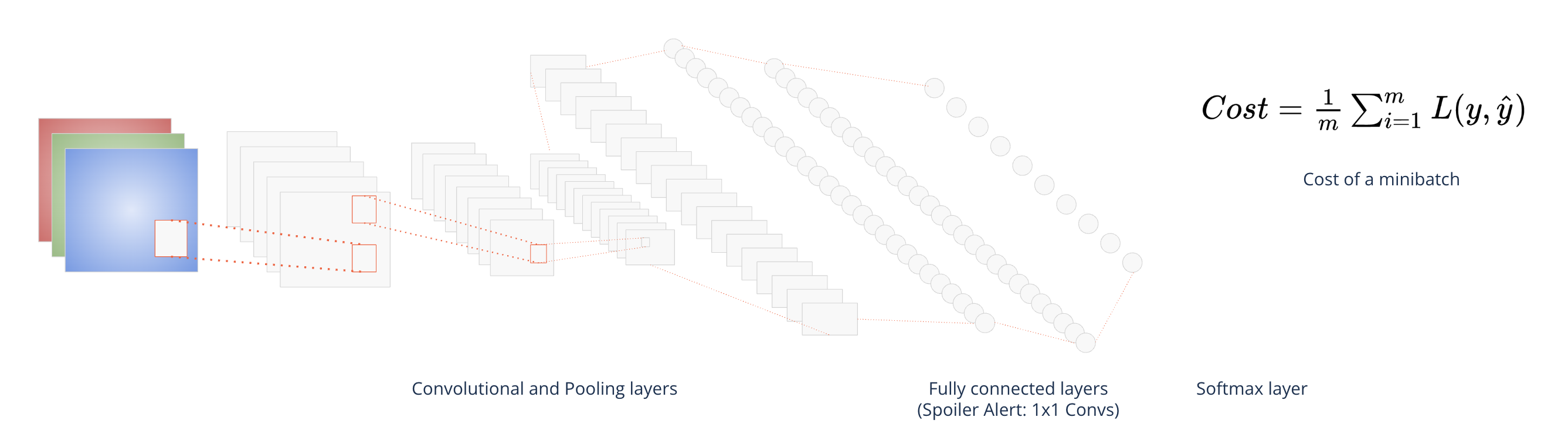
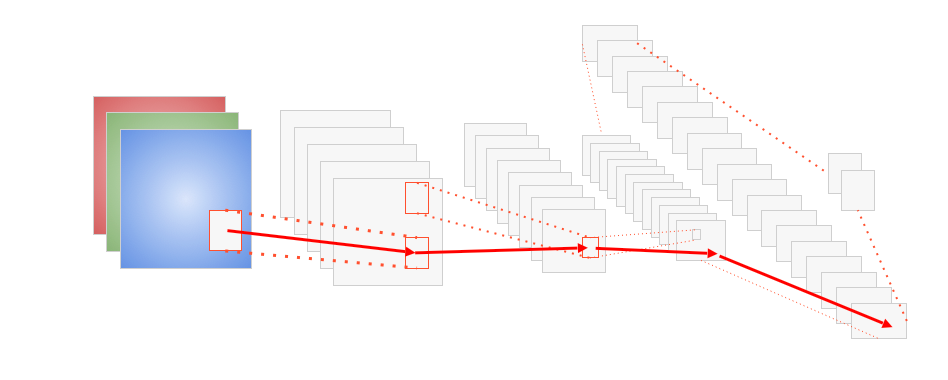
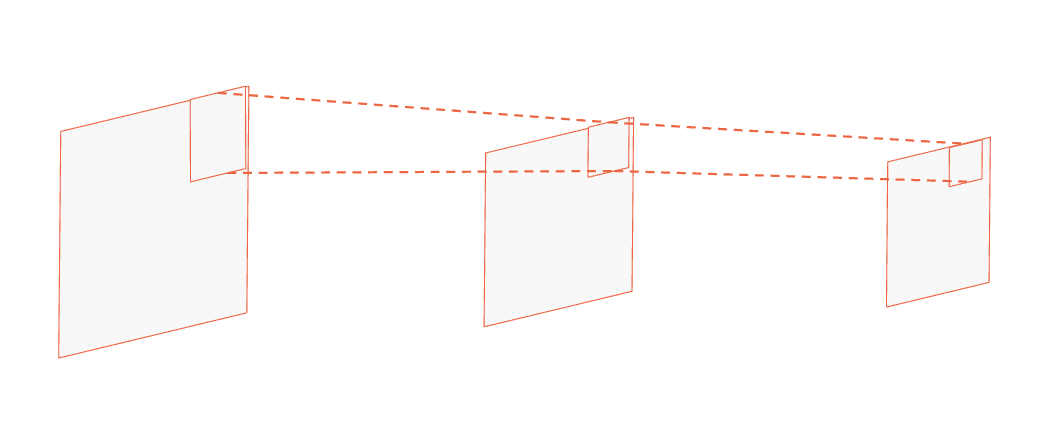
Feature extraction#

  • Hierarchical feature extraction

    • One pixel in deeper layer is connected to many pixels in shallow layer {sparse interactions}

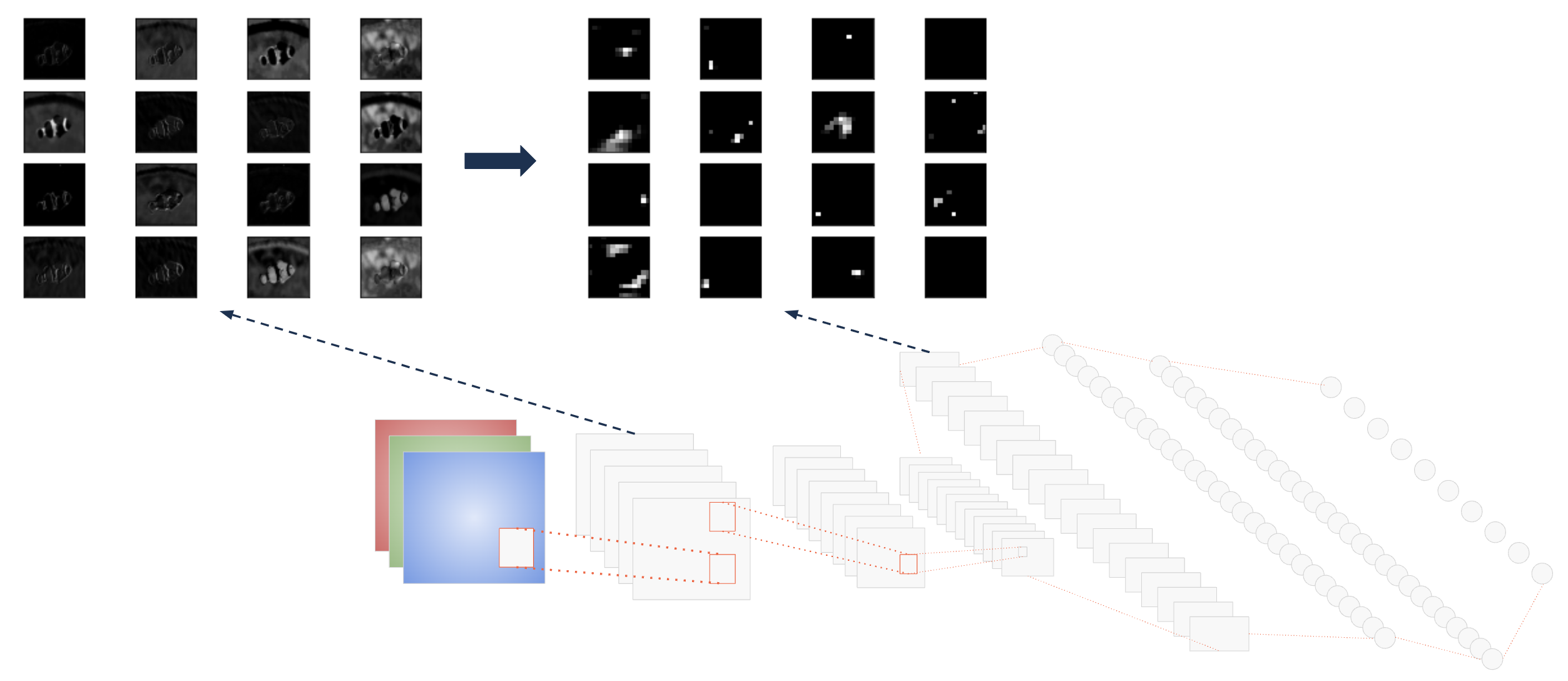
  • Feature complexity grows in each layer

    • First layers learn simple structures, like edges and corners

    • Later layers learn complex structures like eyes, nose, etc.

Feature Extraction#

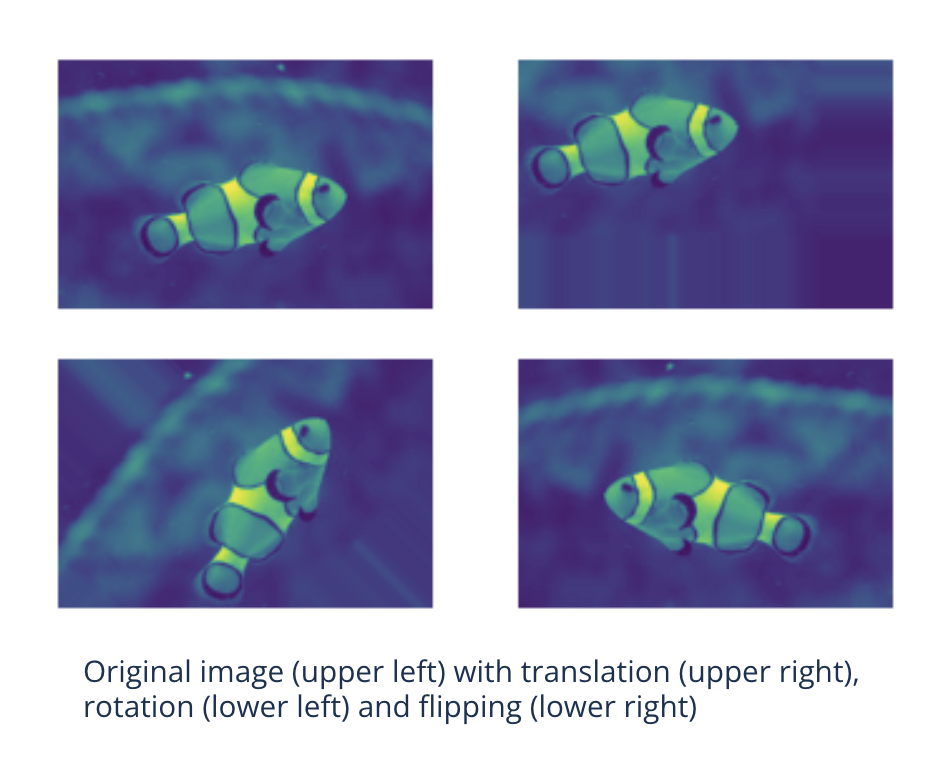
Data augmentation and transfer learning#

Challenges with convolutional neural networks#

  • Deep convolutional neural networks are data hungry

    • Imagine all the features it has to learn from images

  • Data sparsity then is a challenge

    • Could be too less, low-quality, too few variations

  • Two ideas have emerged in the deep learning community to overcome these problems:

    • Data augmentation

    • Transfer learning

Data augmentation#

  • Idea:

    • Randomly transform images during training

      • Translate

      • Rotate

      • Zoom

      • Flip

      • 


  • Enlarges the data set by a significant factor

  • Makes the network more robust

Transfer learning#

  • Human beings learn tasks by transferring knowledge from other tasks they learned before

    • Can ANNs do the same?

  • They can - given some conditions

    • Same input distribution for both tasks

    • Well-learned representations on the first task

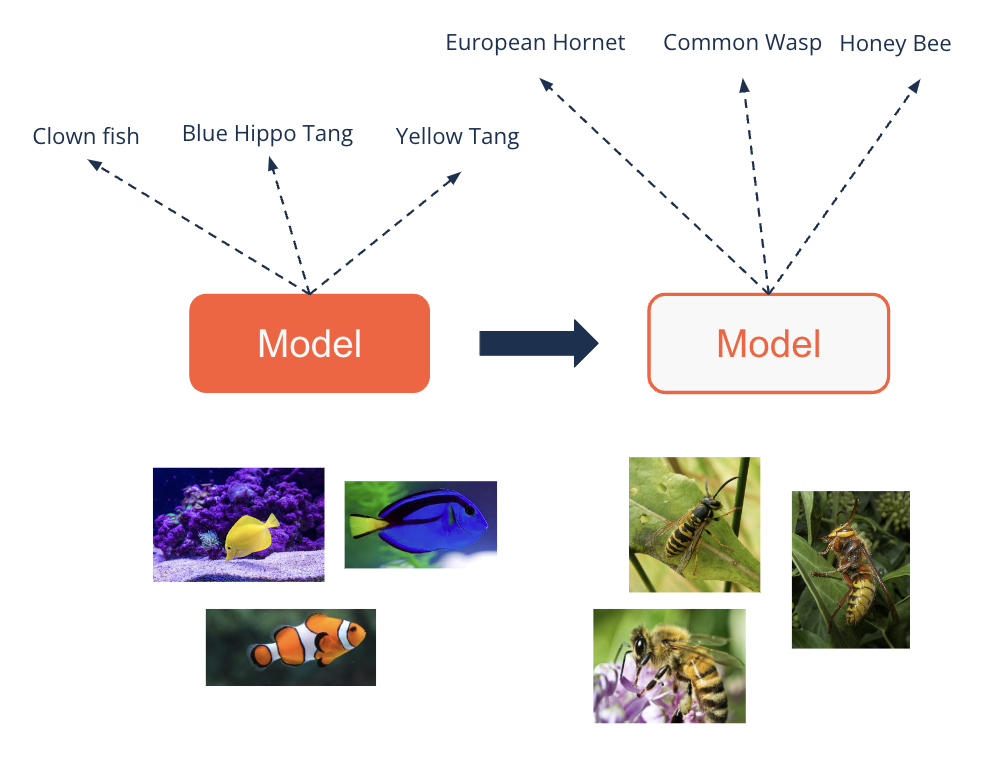
How does transfer learning work?#

  • A model is trained on many data for one task

    • For example classifying fishes

  • Then the upper layers are replaced by a classifier for the second task

    • For example classifying hymenoptera (wasps, bees, etc.)

  • This classifier for the second task gets trained

    • Usually significantly less data is needed for this task

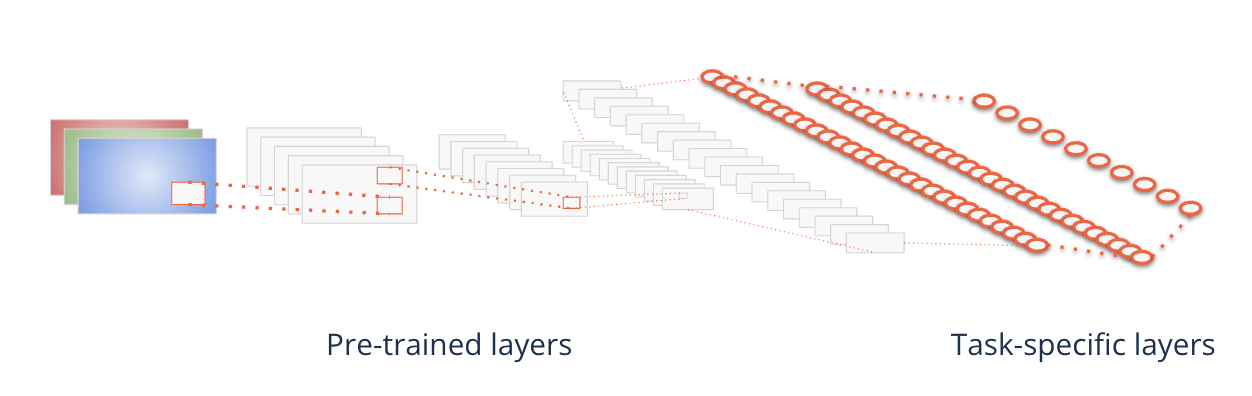
Where do we get pre-trained models?#

Conclusion#

Image Modeling#

  • Image data is unstructured and shows regularly transformations

    • Locality, stationarity, compositionality principle

  • Image models are able to offer translation invariance

  • Special layers in image models are:

    • Convolutional layers: Extract features by filters

    • Pooling layers: Strengthen filter signals and make the net translation invariant

  • Data augmentation helps to increase the data size and robustness of the net

  • Transfer learning enables to use pre-trained models from one task for a second one

Resources#

  • GĂ©ron, A. (2019), Chapter 14: Deep Computer Vision Using Convolutional Neural Networks

  • Li, F.-F. and Johnson, J. (2017), Convolutional Neural Networks for Visual Recognition (much broader, lectures 1-5)

Image Feature Engineering:

  • Dalal, N. and Triggs, B. (2005), “Histograms of Oriented Gradients for Human Detection”, CVPR 2005. IEEE Computer Society Conference on. IEEE, 2005. S. 886–893

  • Lowe, D. (1999), “Object Recognition from Local Scale-Invariant Features”, ICCV ‘99 Proceedings of the International Conference on Computer Vision. Band 2, Seiten 1150–1157.

  • Lowe, D. (2004), “Distinctive Image Features from Scale-Invariant Keypoints”, International Journal of Computer Vision. Band 60, Nr. 2, Seiten 91–110, 2004

  • Bay, H. et al. (2006), “SURF: Speeded Up Robust Features”, European Conference for Computer Vision 2006

Drawbacks of deep neural networks:

  • Hornik (1991), “Approximation Capabilities of Multilayer Feedforward Networks”

  • CsĂĄji (2001), “Approximation with Artificial Neural Networks”

ImageNet Competition:

  • Perronin and Sanchez (2011), “Compressed Fisher Vectors for LSVRC”

  • Krizhevsky et al. (2012), “ImageNet Classification with Deep Convolutional Neural Networks”

Strive:

  • Springenberg et al. (2015), “Striving for Simplicity: The All Convolutional Net”

  • Kong and Lucey (2017), “Take it in your stride: Do we need striding in CNNs?”

Data Augmentation:

  • LeCun et al. (1998), “Gradient-Based Learning Applied to Document Recognition”

  • Krizhevsky et al. (2012), “ImageNet Classification with Deep Convolutional Neural Networks”

  • Wang, J. and Perez, L. (2017), “The Effectiveness of Data Augmentation in Image Classification Using Deep Learning”

Transfer Learning:

  • Caruana, R. (1995), “Learning Many Different Tasks at the Same Time with Backpropagation”

  • Yosinski, J. et al. (2014), “How transferable are features in deep neural networks?”

  • Weiss, K. et al. (2016), “A survey of transfer learning”

Feature Extraction:

  • Garcia, D. et al. (2018), “On the Behavior of Convolutional Nets for Feature Extraction”

  • Zeiler, M.D. and Fergus, R. (2014), “Visualizing and Understanding Convolutional Networks”

  • Yosinski, J. et al. (2015), “Understanding Neural Networks Through Deep Visualization”

Contents