Exploratory Data Analysis

Exploratory Data Analysis#

Table of Content#

  • The EDA Process put into context

  • Types of EDA

    • uni-/bi-/multi-variate

    • numerical vs. graphical

    • continuous vs. categorical data

  • Measures of central tendency / dispersion

  • Distribution functions / histograms / modality

  • Correlations

  • Special considerations for categorical / discrete variables

  • Summary / References

The EDA Process#

Research / Business Questions#

Those questions that arise from a researcher guessing about reality (data). They are written in the form of a question.

Examples:

  • Which factors can increase ice cream sales?

  • Can we predict skin cancer using photographs of the melanome?

  • How does the material composition of a bridge affect its durability?

Hypothesis Generation#

  • Hypotheses are assumptions or educated guesses we make about the data, using our domain knowledge.

  • You can form a hypothesis in the form of “if/then” or “the more the”.

  • A Hypothesis is formed as a measurable (operationisable) statement you can validate by looking at data.

  • A research question can have multiple hypotheses attached to it.

Examples:

  • If the sun is shining then ice cream sales increase.

  • The larger the melanoma, the greater the risk that it is malignant.

  • The cheaper the material composition the shorter its durability.

Hypothesis Generation != Hypothesis testing#

The process is an educated guess, the hypothesis could still come out to be true or false after EDA and hypothesis testing (is the conclusion random or not?)

Hypothesis testing

Where does EDA belong in the bigger picture?#

Black cats and domain experts#

The hardest thing of all is to find a black cat in a dark room, especially if there is no cat.


→ Talk to domain experts or become one.

What is EDA and why do we do it?#

What is EDA?#

→ Detective work

EDA is the process of summarizing and visualising important characteristics of the data in order to gain insights.

It’s an approach/process not a set of techniques.

Tools:

  • Any method of looking at data that does not include formal statistical modelling and inference

  • Visualisation

Note:

Confirm the expected or show the unexpected!

Goals and Benefits#

  • Understand each variable

  • Get insight into relationships between the variables

  • Draw valid conclusions

  • Checking assumptions

  • Aid in decision making and planning

  • Help in causal analysis

→ To build intuition about the data and gain insights

→ To generate and corroborate or reject hypotheses

Types of EDA#

  • Univariate or multivariate

  • Graphical or non-graphical

  • Dealing with both categorical and numerical data

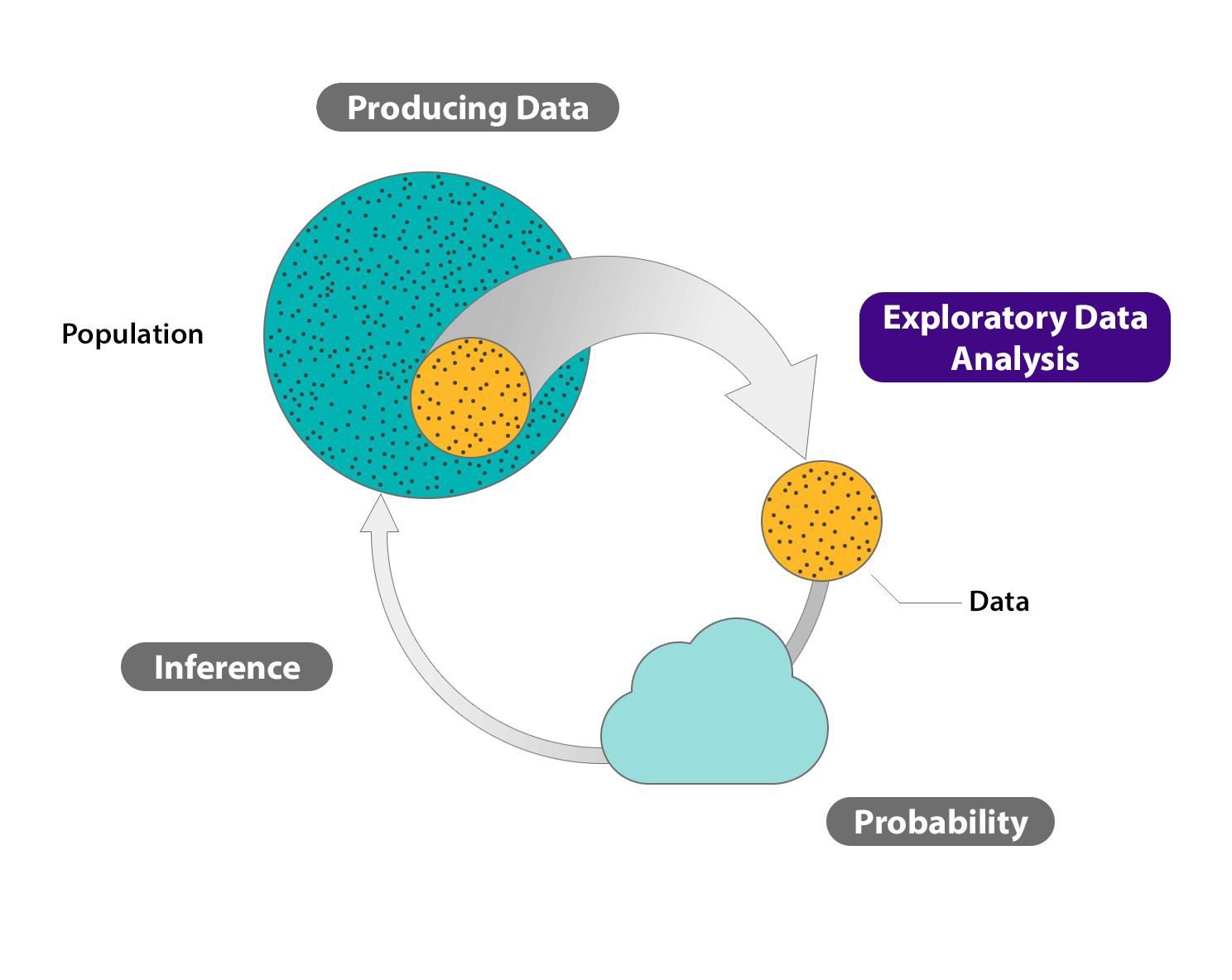
Estimates#

  • We can rarely have money/resources to measure everything

  • So we will have samples of the population which we hope to be representative of the whole population

  • The more data we have the more confident we are in the estimates

  • Ideally: the results drawn from our experiments are reproducible

Note:

In Data Science most metrics omit the “estimate” word… nevertheless mostly all metrics we use are estimates.

Univariate vs. Multivariate Analysis#

Univariate Analysis:

  • Analysis of a single variable (often called feature)

  • Characterises data by focusing on distribution, central tendency, dispertion, etc

  • Represents information numerically and visually

Multivariate Analysis:

  • Simultaneous analysis of multiple variables

  • Examines how changes in one variable are associated with changes in others

  • Characterises dependence by a numerical coefficient

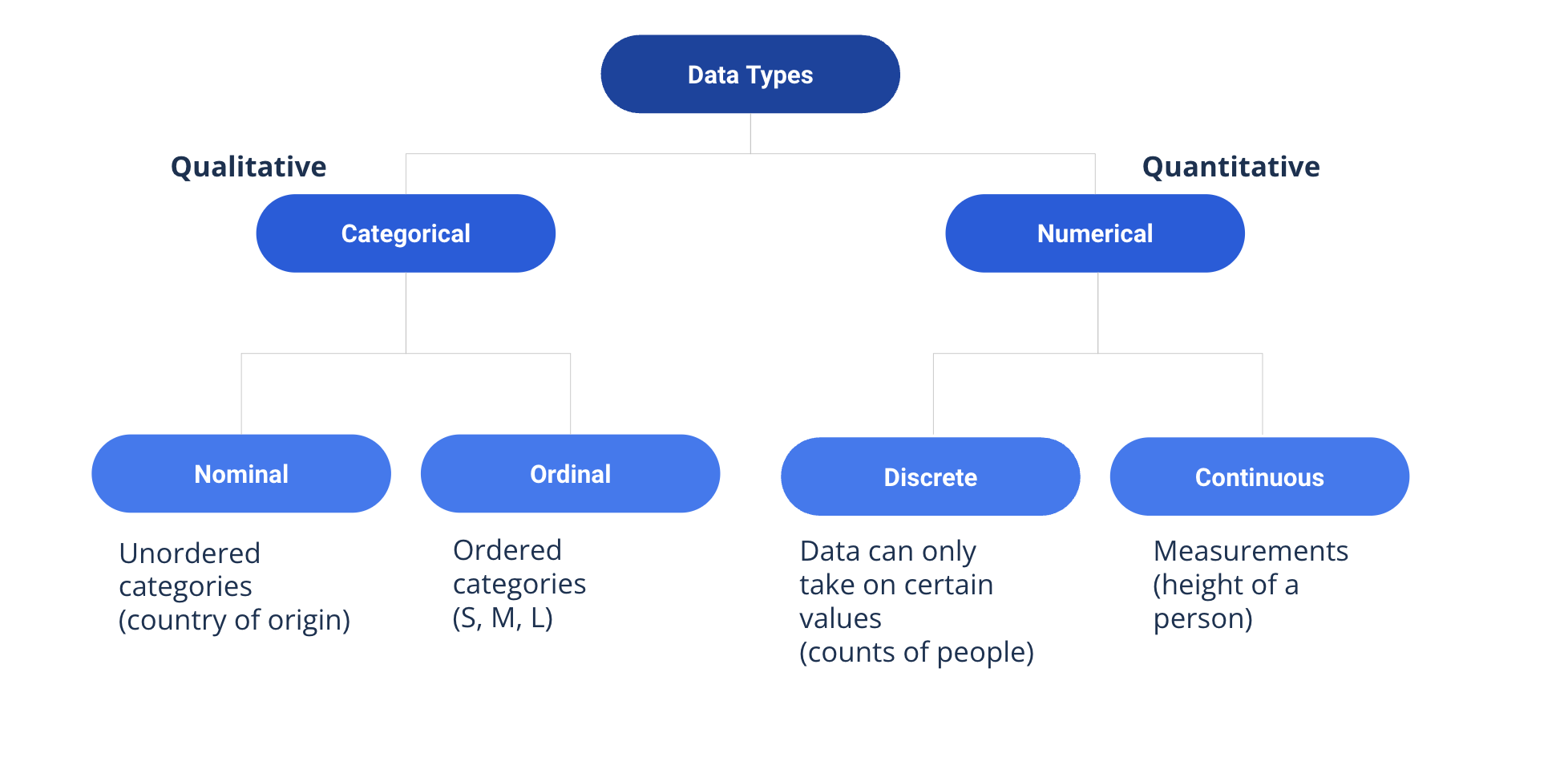
→ Description and understanding of individual variables
→ Understanding of the relationship and interaction among multiple variables

Data Types#

Univariate EDA#

Describing Central Tendency#

Mean#

  • sum of data points divided by number of data points

  • often used as default

  • sensitive to extreme values

What is the mean in this example?

id

y

1

2

2

6

3

6

4

8

5

10
\[\bar{y}=\frac{1}{n} \sum\limits_{i=1}^{n}y_{i}\]

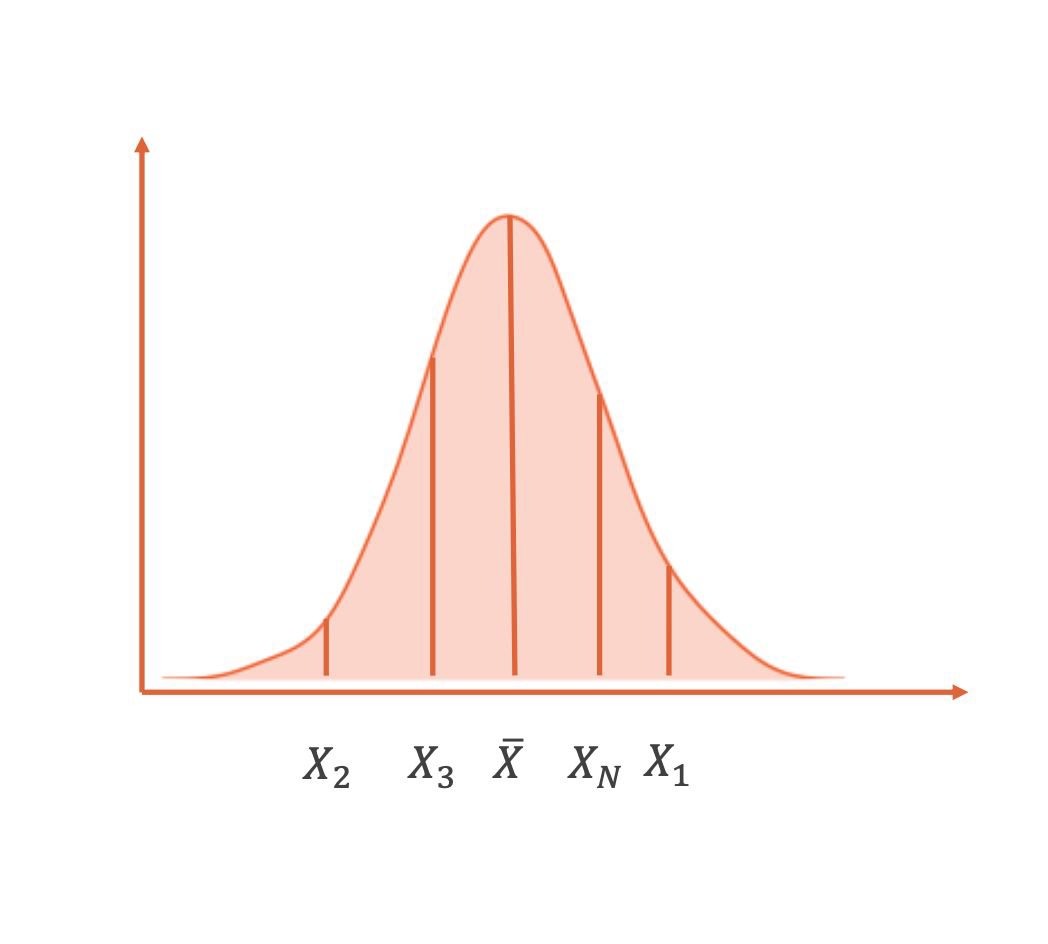
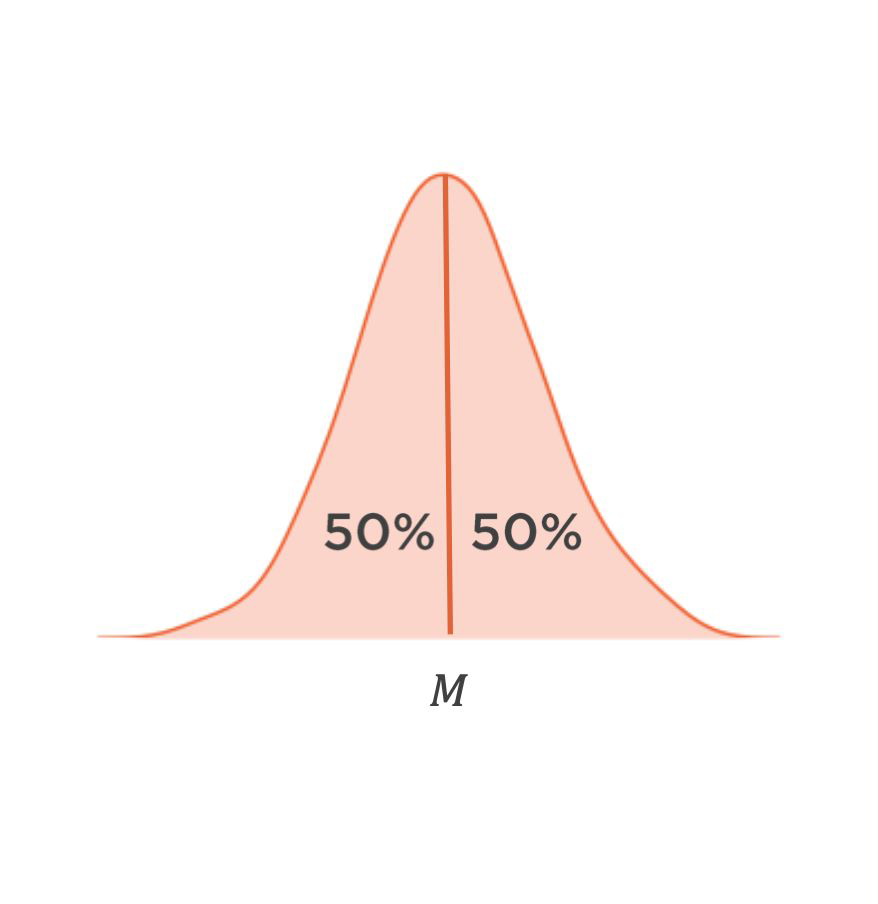
Median#

  • value in the middle of a data series ordered by size

  • more robust against extreme values but computationally more expensive since values need to be sorted

What is the median in this example?

id

y

1

2

2

6

3

6

4

8

5

10
\[\begin{split} y_{i} \leq y_{i+1}\;\text{for}\;i=1,...,n-1 \\ y_{\frac{n+1}{2}}\;\text{if}\;n\;\text{is odd} \\ \frac{1}{2}\big(y_{\frac{n}{2}}+y_{\frac{n+1}{2}}\big)\;\text{if}\;n\;\text{is even} \end{split}\]

Mode#

  • most frequent values

  • not necessarily unique

  • mostly used for categorical data

What is the mode in this example?

id

y

1

2

2

6

3

6

4

8

5

10

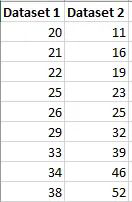
Describing the Spread#

Range#

  • difference between largest and smallest value

  • measures the spread of the data

  • sensitive to outliers

Which dataset has the larger range?

Quantiles#

  • quantiles split sorted data into parts with equal amount of observations

    • quartiles: splits data into 4 parts

    • deciles: splits data into 10 parts

    • percentiles: splits data into 100 parts

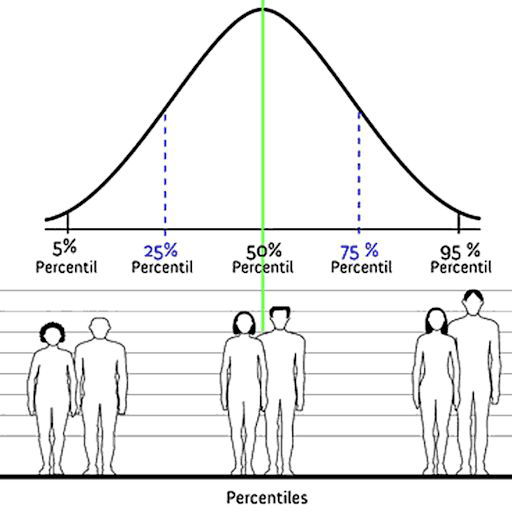
Notes: The position of the percentiles are not equidistant (and depend on the distribution)

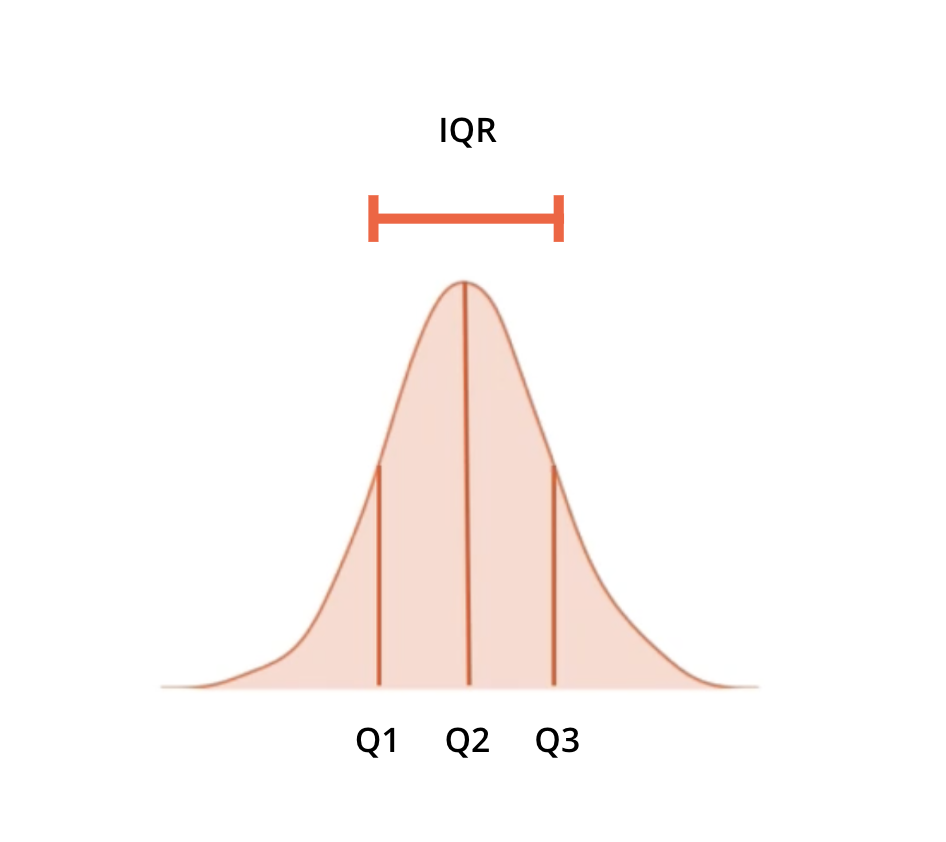
Interquartile Range (IQR)#

  • width of interval that contains the middle 50% of the data

  • interval between the 25th and 75th percentile

  • interval between 1st and 3rd quartile

  • robust to outliers

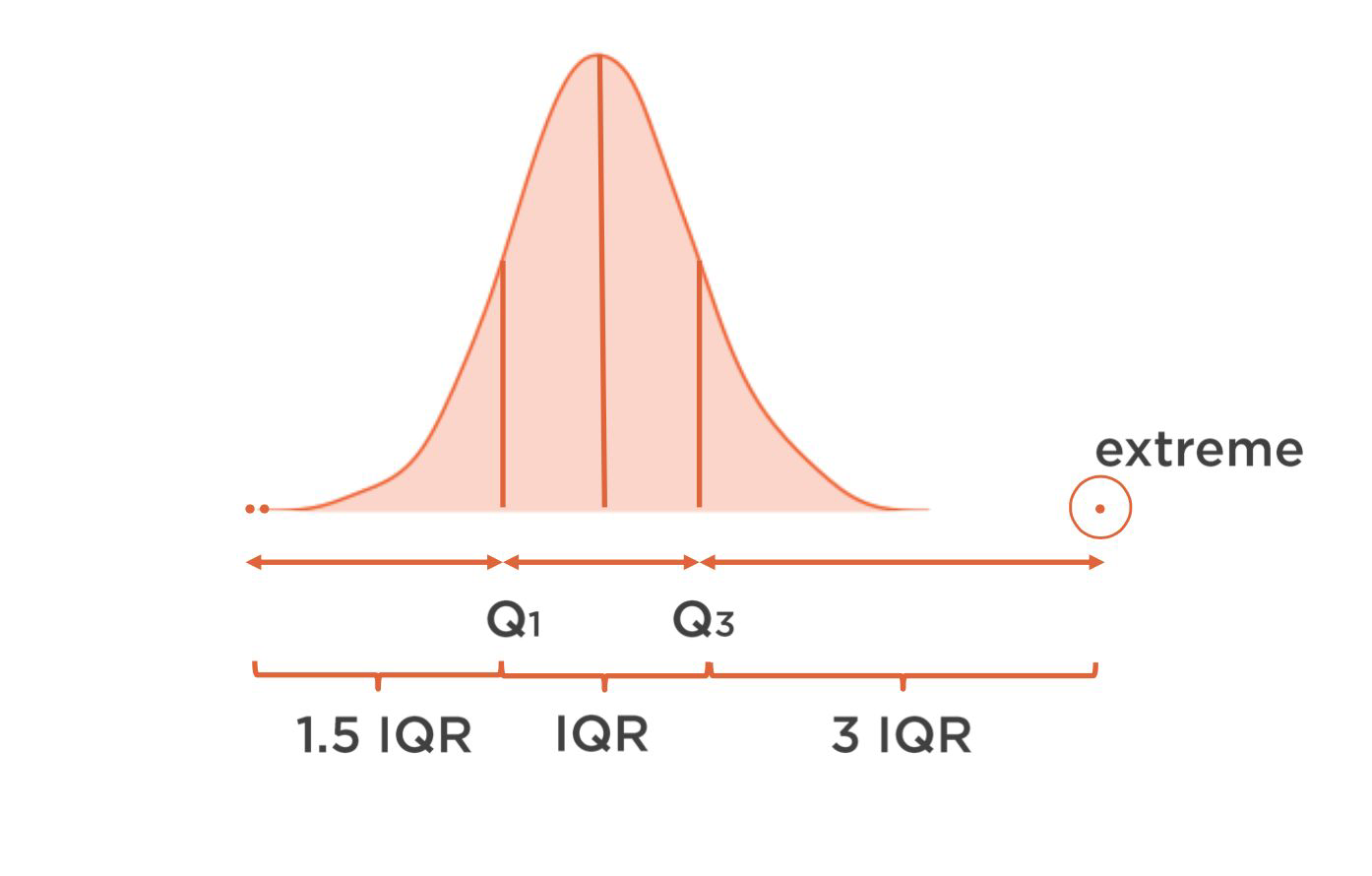
Outliers#

  • No generally recognized formal definition for outlier

  • Values outside of the areas of a distribution that would commonly occur

Note:

If an outlier is good or bad depends on the data problem. For example for anomaly detection you want to keep outliers.

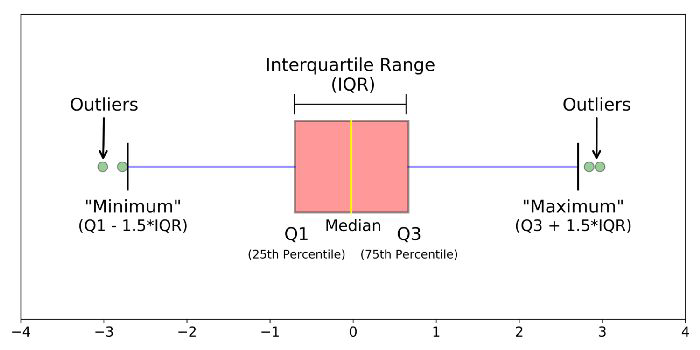
Box Plots#

Variance & Standard Deviation#

Variance

  • average squared difference of the values from the mean: \( \sigma_{sample} = \frac{1}{n-1}\sum_i{(x_i-\bar{x})^2}\)

Standard deviation

  • square root of variance: \(SD = \sqrt{\sigma}\)

  • standard difference between each data point and the mean

  • has the same unit as the original data

Both are not robust to outliers.

degrees of freedom

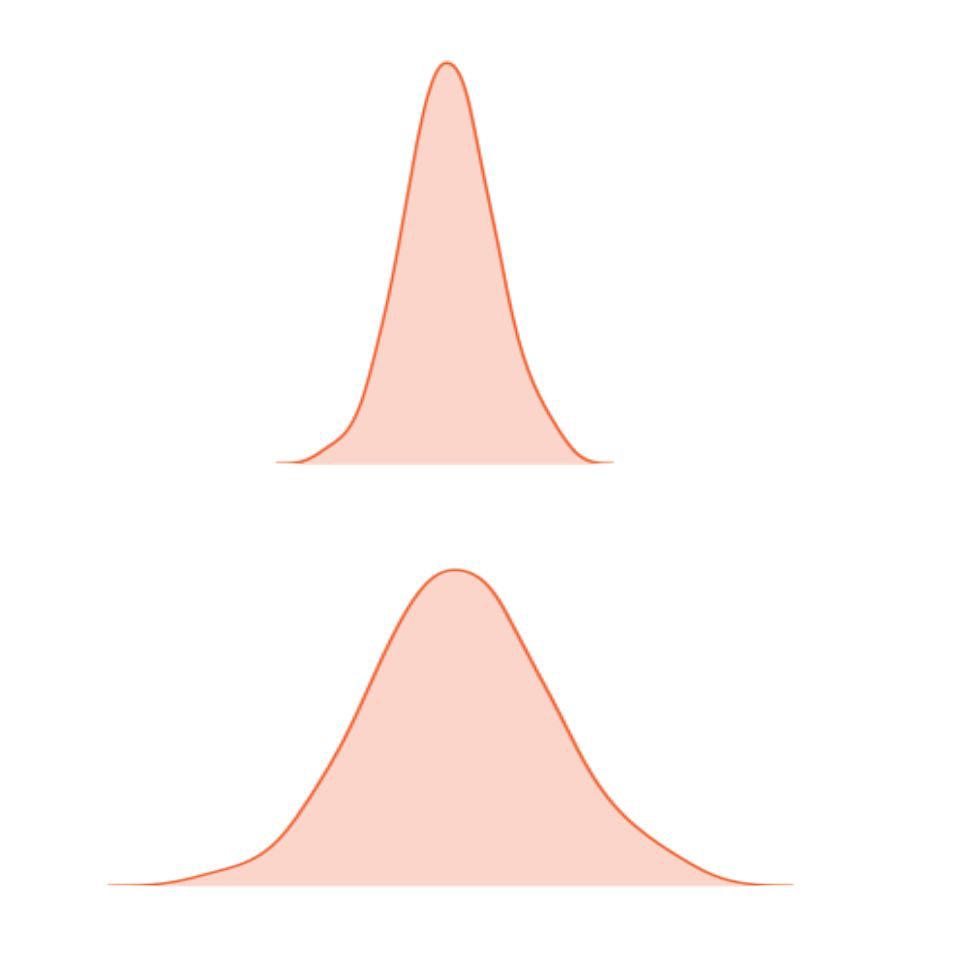
Describing the Distribution#

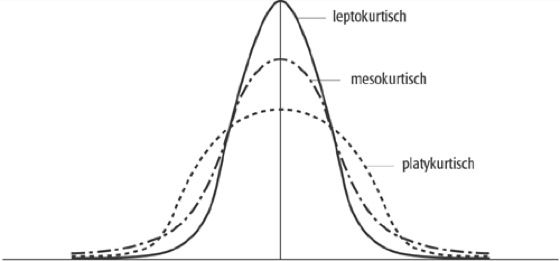
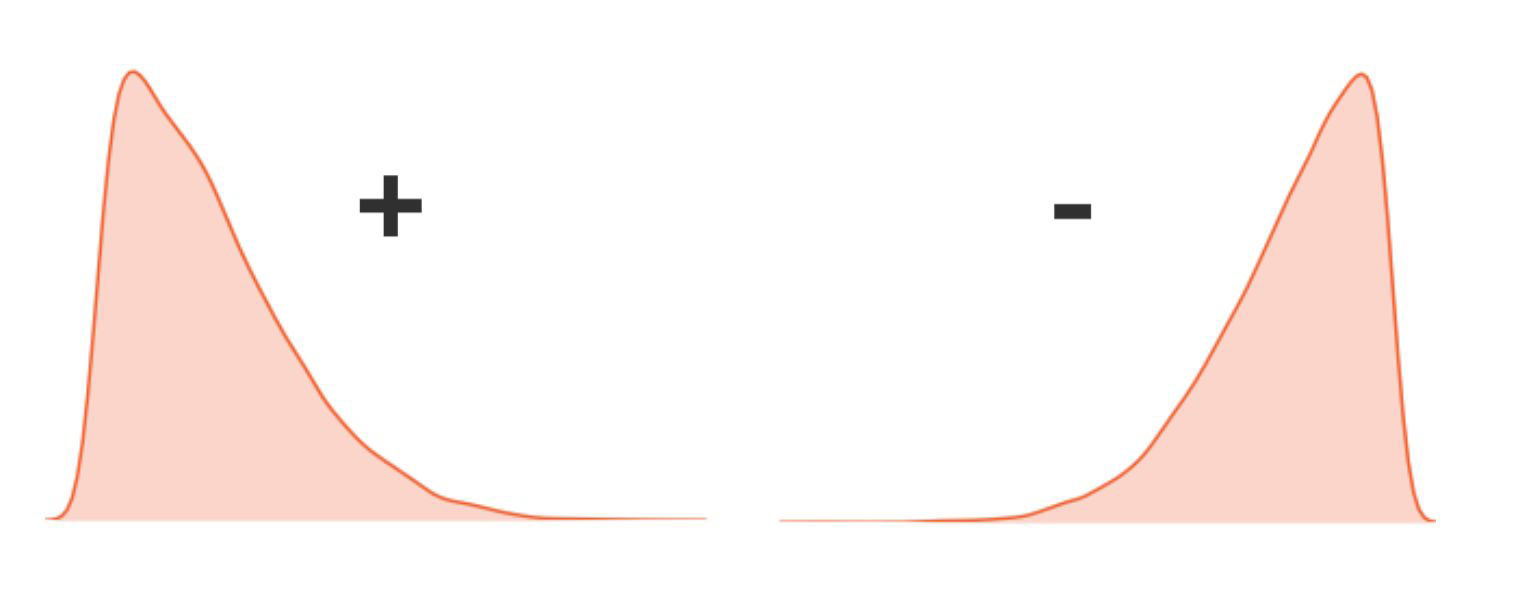
Skewness & Kurtosis#

Skewness

  • degree of asymmetry of the distribution of the data

Kurtosis

  • degree of pointyness relative to a normal distribution (flat vs. pointy)

Kurtosis

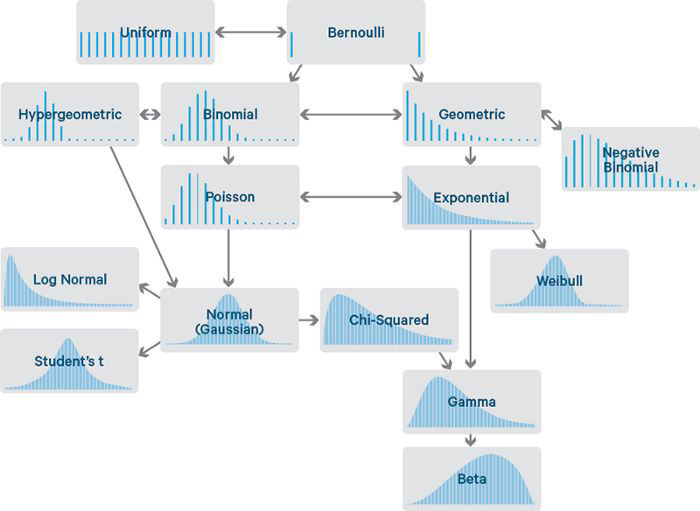
Data Distributions#

  • Uniform
    all events have same frequency, e.g. outcome of a dice roll

  • Bernoulli
    two possible outcomes, e.g. a coin toss

  • Binomial
    “discrete version” of normal distribution, e.g. 100 x two coins: likelihood of a certain number of only heads

  • Normal
    most continuous real-valued variables in nature follow this distribution

  • Poisson
    events occurring at random points of time and space - the number of events Video

  • Exponential
    the interval between events

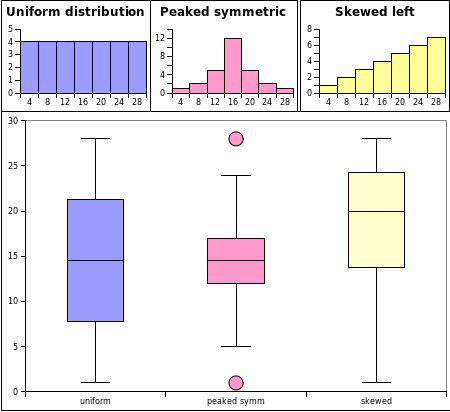
Visualising Data Distributions with Histograms#

Box Plots#

What do we see here?

Binwidth#

  • Binwidth matters!

  • Same data with bin width = 5, 2, 1

Note:

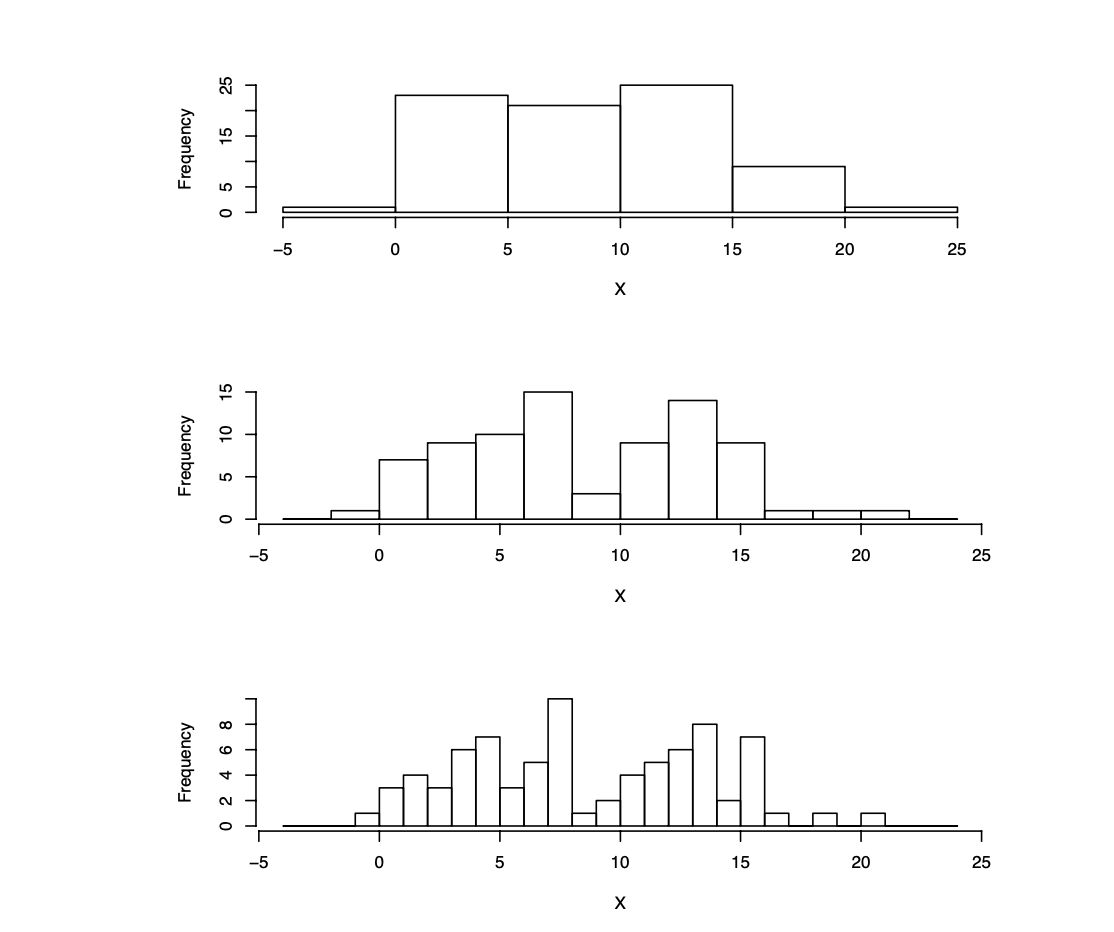
Rule of thumb: Take the square root of the sample size as the number of bins for a first guess (trial and error).

How to choose number of bins#

Rule of thumb: Take the square root of the sample size as the number of bins for a first guess (trial and error).

Consider:

  • too large bins → we lose details or end up having only one bin

  • too small → we have too much detail or end up with one bin per observation

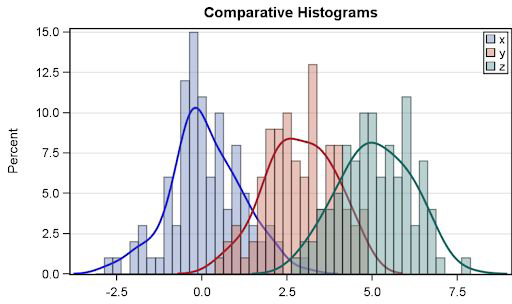
Comparing Data Distributions with Histograms#

Histograms:

  • Good for looking at residuals (variance)

  • Works best for comparing max 3-4 groups

  • You can use so-called kernel density estimates (KDE) to plot it continuously

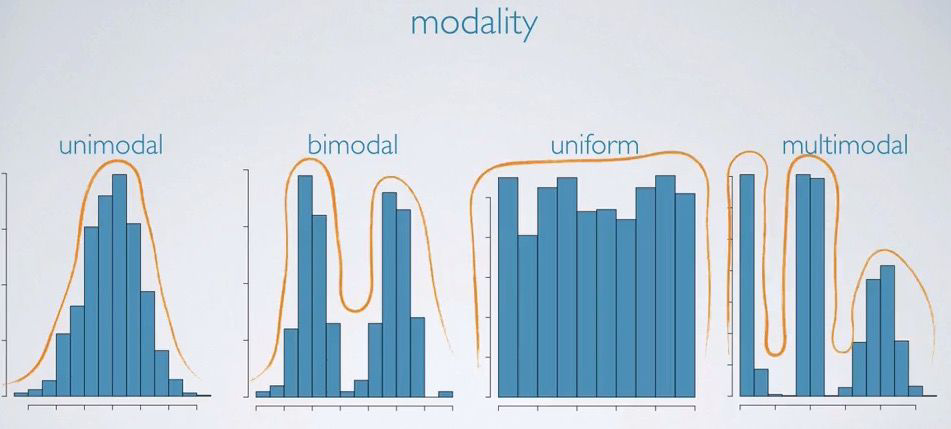
Modality#

  • Plot a histogram and look at the number of peaks in the distribution

Data Summaries#

Central tendency

Spread

Modality

Shape

Outliers

mean

range

unimodal

skewness

median

interquartile range

bimodal

kurtosis

mode

variance

multimodal

quantiles

standard deviation

uniform

Multivariate EDA#

Numerical Data#

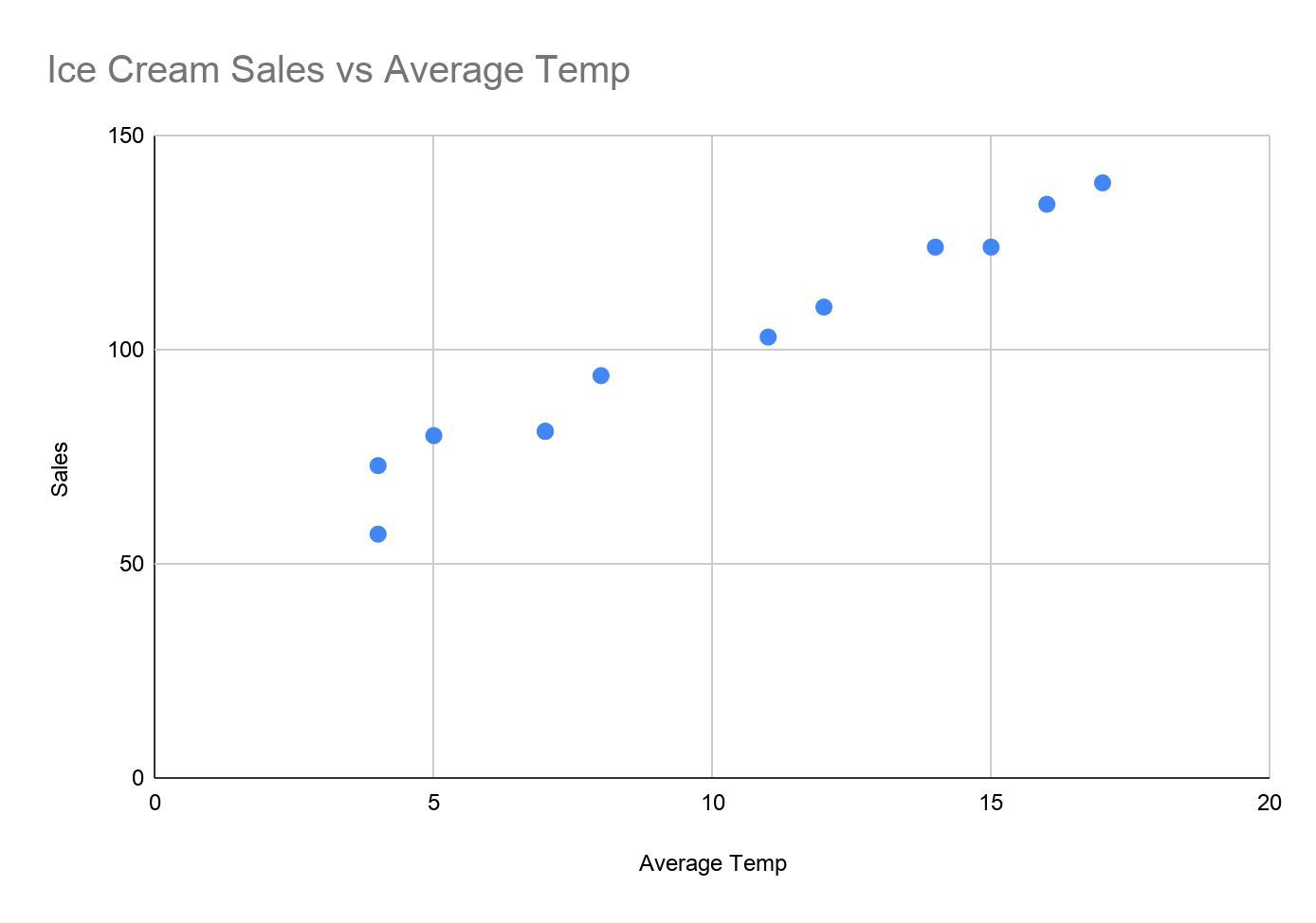
Scatter Plot#

  • Used to visualise relationship between two numeric variables

  • Also called correlation plots

  • Can encode multiple dimensions by color and size

It visually answers the question:

→ “How are these variables related?”

→ “When variable X grows, what happens to variable Y? With which intensity?”

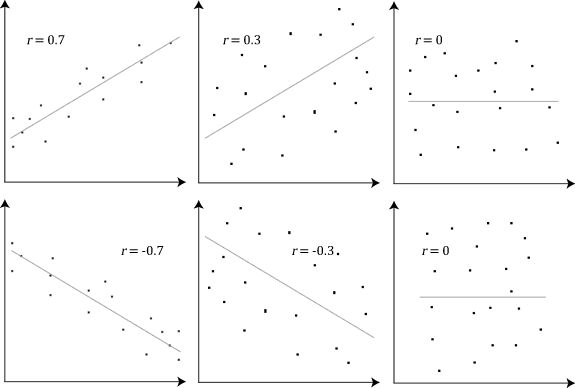
Pearson correlation coefficient / Pearson’s r#

  • Measures the linear relationship between two variables

  • Ranges between -1 and 1

→ close to 1: strong positive linear relationship

→ around 0: no linear relationship

→ close to -1: strong negative linear relationship

guess the correlation

The ice cream example#

Month

Average Temp

Sales

January

4

73

February

4

57

March

7

81

April

8

94

May

12

110

June

15

124

July

16

134

August

17

139

September

14

124

October

11

103

November

7

81

December

5

80

The ice cream example#

r = 0.983

Note:

A correlation analysis may establish a linear relationship but does not allow us to use it to predict the value of a variable given another. Regression analysis allows us to this and more.

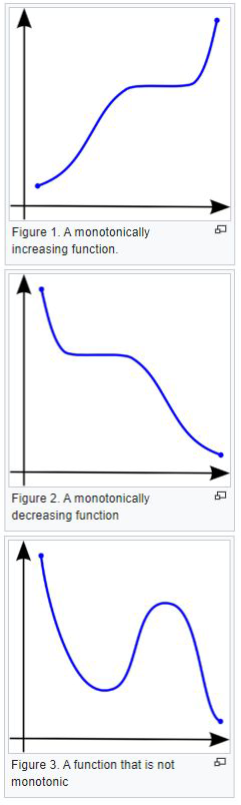
Spearman rank correlation coefficient - Spearman’s ρ#

  • Measure of rank correlation, it is based on the rank of the values vs. the raw data

  • Represents the strength of a monotonic relationship

Monotonic function:

→ increasing: as X increases Y never decreases

→ decreasing: as X increases Y never increases

Consideration about correlation#

  • If two variables are independent, their correlation is 0, but a correlation of 0 does not imply that two variables are independent!

  • The correlation coefficients cannot replace visual examination of data.

  • The presence of correlation is not enough to infer causation!

Bivariate and Multivariate Analysis#

Looking at all possible combinations of features:

  • for 9 features bivariate would mean 36 combinations: \(\sum_{i=1}^{8} i\)

  • How do we reduce the exploration space or focus on interesting combinations?

Correlation Matrix

Special consideration of discrete / categorical data#

  • mode

  • frequency tables: number of times a value occurs

  • expected values: weighted mean when categories can be associated with numerical value

Frequency tables#

  • Tabulation of the frequencies

  • Show the range of values and frequency of occurrence

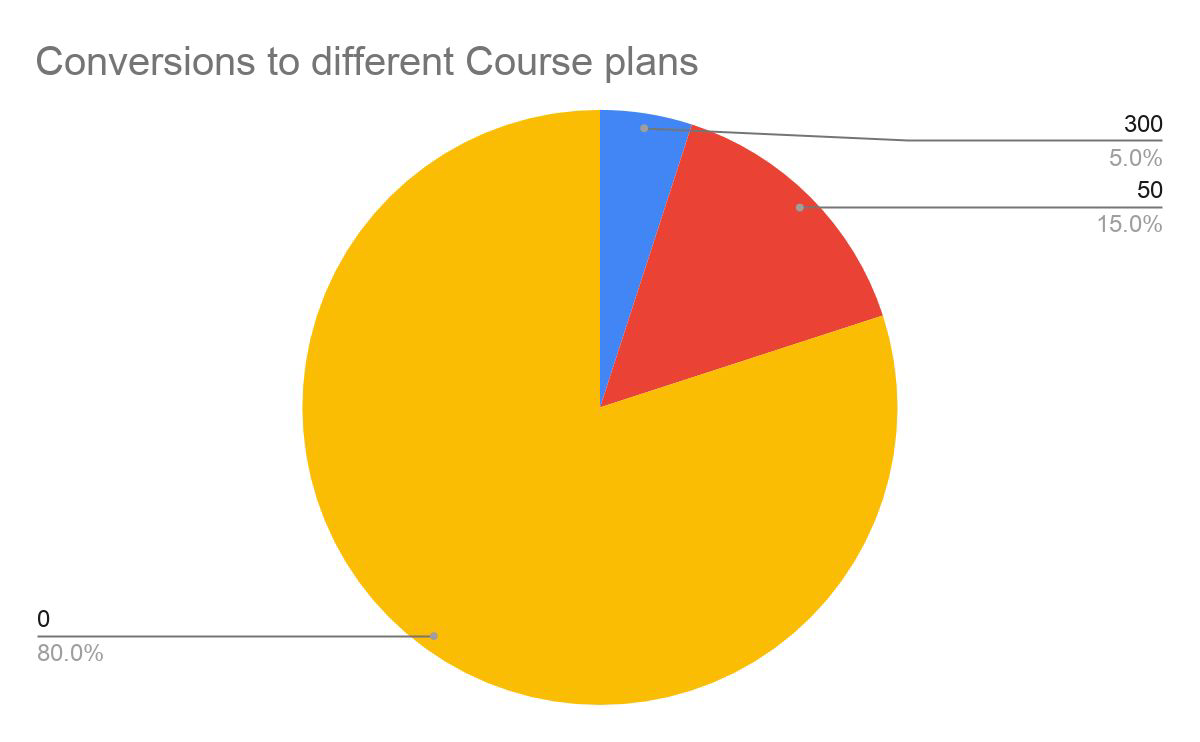
Expected values#

  • weighted mean

Example: Offers for different course plans for financial purposes we can sum this up in a single “expected value,” which is a form of weighted mean, in which the weights are probabilities.

\(EV = 0.05*300 + 0.15*50 + 0.80*0 = 22.5\)

Cross-tabulation#

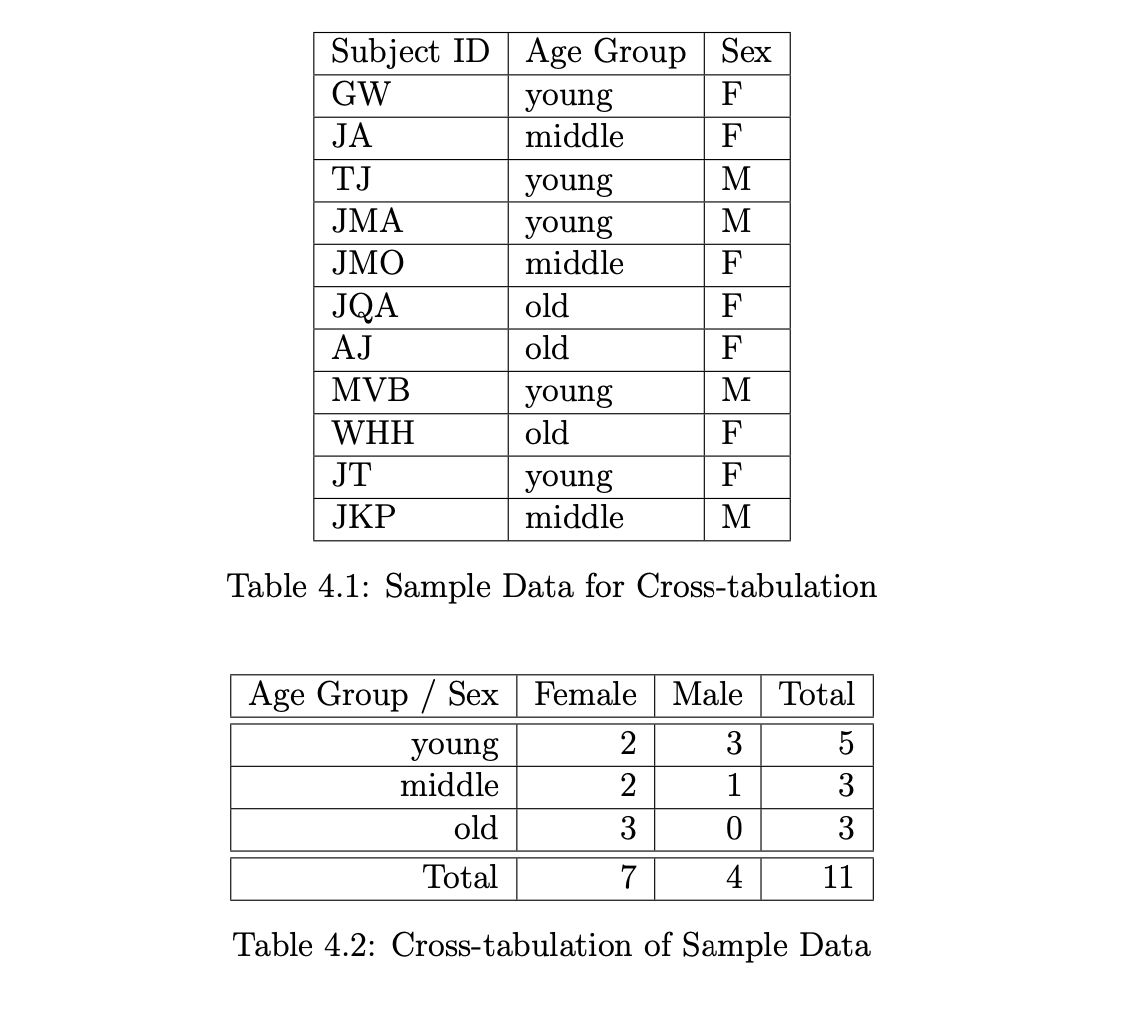
Summary / Outlook#

EDA is like a detective’s investigation to

  • understand the data

  • identify patterns

Why do we want to know our data? Because we want to find out

  • how to answer our research / business question

  • whether the data is suitable / sufficient

  • how to answer the research questions with the existing data

  • how to phrase/refine our hypotheses

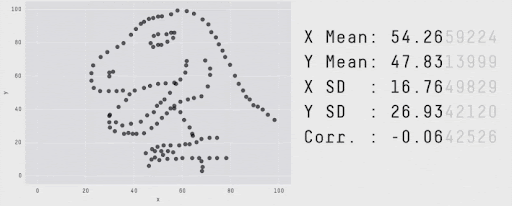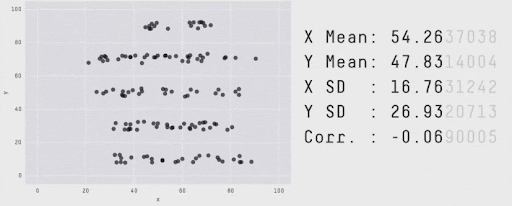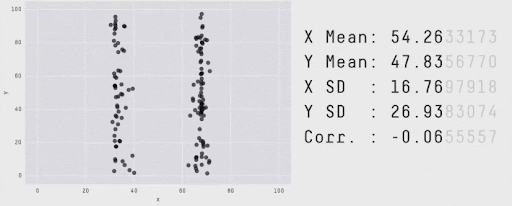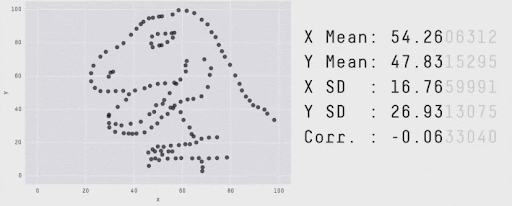
Summaries vs. Details…#

Techniques Map#

Techniques Map

Visual Vocabulary#

Visual Vocabulary

References#

Contents