KNN & Distance Metrics#
Recap on general concepts#
What’s the difference between supervised and unsupervised learning?#
 Supervised Learning vs. Unsupervised Learning
Supervised Learning vs. Unsupervised Learning
What are the two different tasks that can be solved with supervised learning?#

The KNN Algorithm#
Overview of KNN#
KNN is a supervised learning algorithm
used to solve both regression and classification problems
KNN assumes that similar things exist in close proximity
→ “Birds of a feather flock together”

Why using KNN?#
Despite its simplicity, it was often successful for both classification and regression problems:
handwritten digits
satellite image scenes
it’s good for situations where decision boundary is very irregular
How would you classify the question mark?#
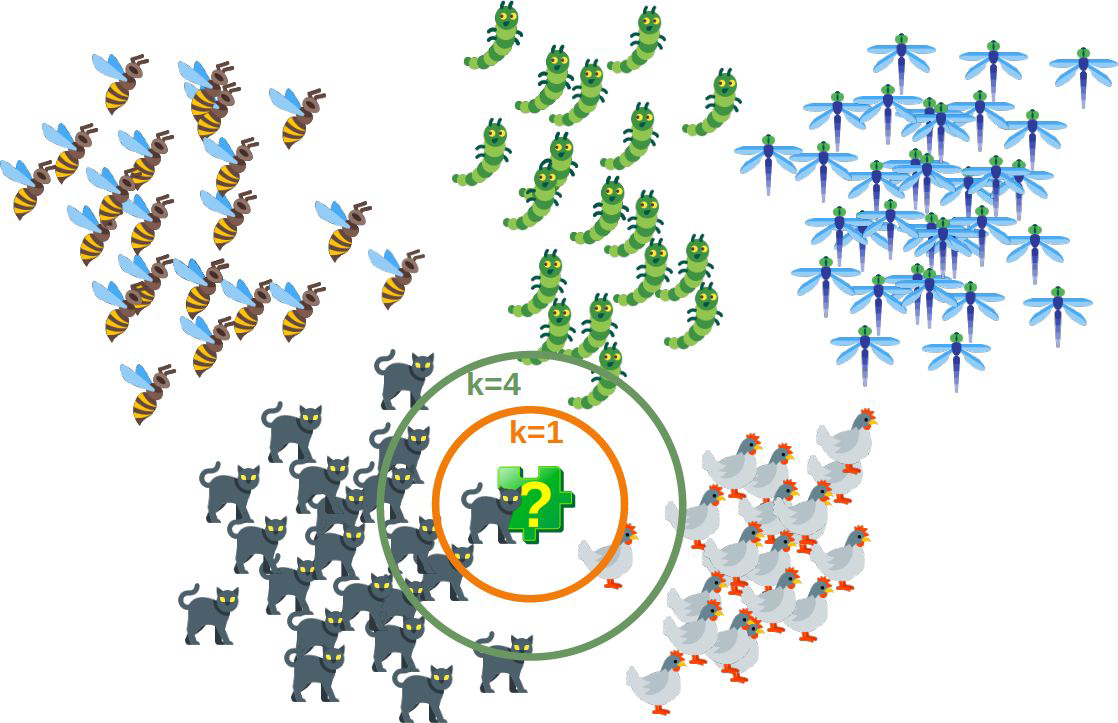
How to measure “close proximity”?#
KNN is based on the idea of “similarity”
mathematically speaking similarity can be calculated via distances
simplest distance would be the line distance → Euclidean Distance
KNN#
Input:
data with features that are comparable (i.e. can calculate a distance) & target variable
How KNN works:
loop over the observations:
calculate distance to all (brute force) or some (optimized) data points
sort them and pick K “closest”
Output:
Regression: the mean of the neighbors
Classification: the mode of the neighbors
How to train KNN?#
What’s happening when we call knn.fit():
training phase consists of “remembering” / storing all data points
→ training time is very short

How to predict for new instances?#
calculate distance between new observations and every training data point
K closest points are determined
test data are assigned to the class of their K nearest neighbors according to majority voting
→ prediction time can be very high
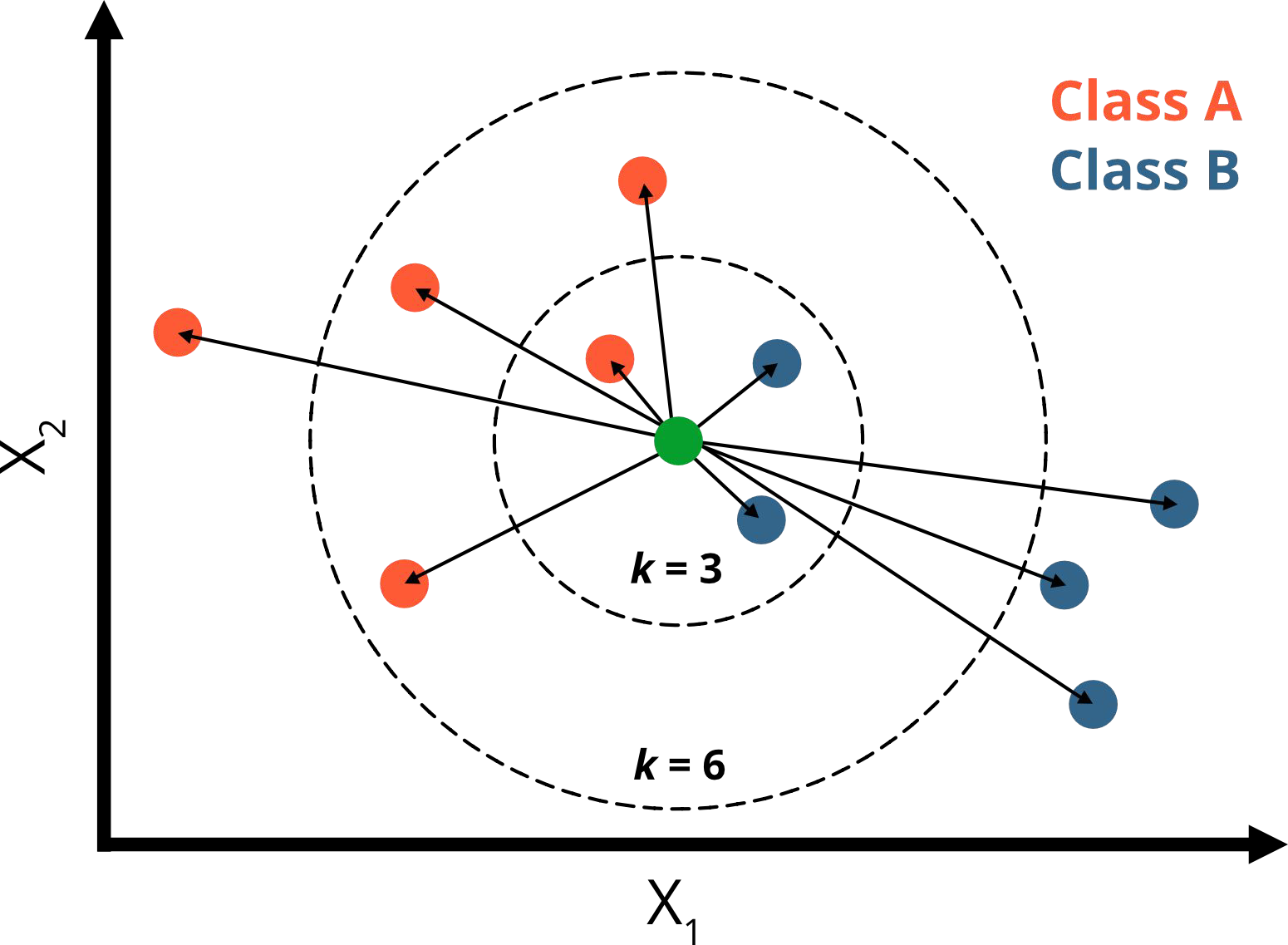
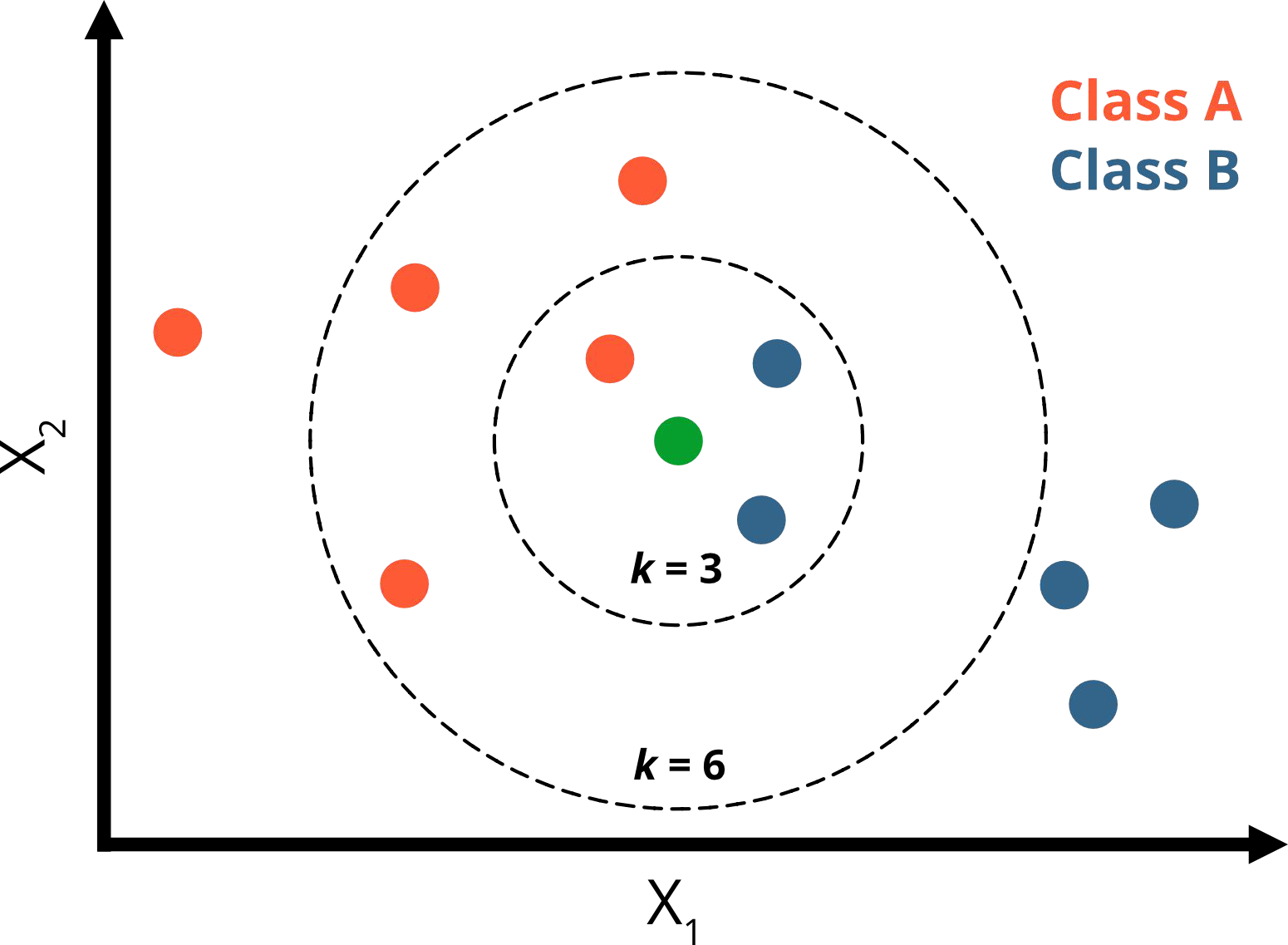
What would you predict for k = 3 and k =6 ?
How to predict for new instances?#
k = 3:
1 neighbor is orange (p=⅓)
2 neighbors are blue (p=⅔)
→ green point belongs to class B
k = 6:
4 neighbors are orange ( p=⅔)
2 neighbors are blue (p=⅓)
→ green point belongs to class A

What are the assumptions of KNN?#
similar observations belong to the same class / have a similar outcome
no assumption is made on data distribution / mapping function
→ KNN is a non-parametric algorithm
What are some assumptions of linear regression?
Hyperparameters#
What influences the performance of KNN?#
What are hyperparameters of KNN?#
The number of neighbors (K) which is taken to classify.
The distance metric used to determine the nearest neighbors.
The weight applied to neighbours during prediction phase.
Influence of K#
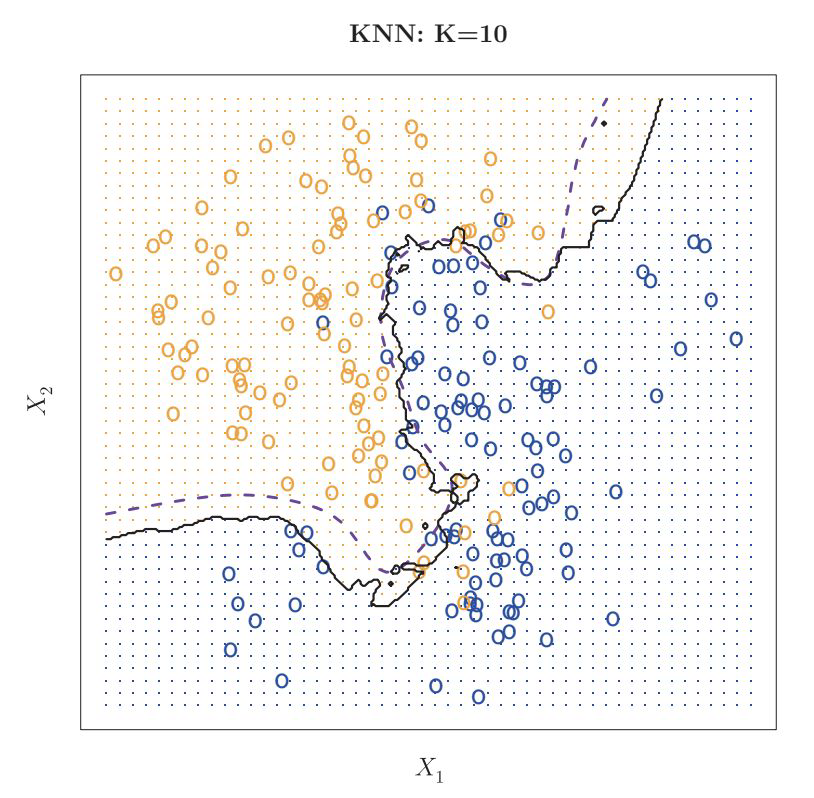
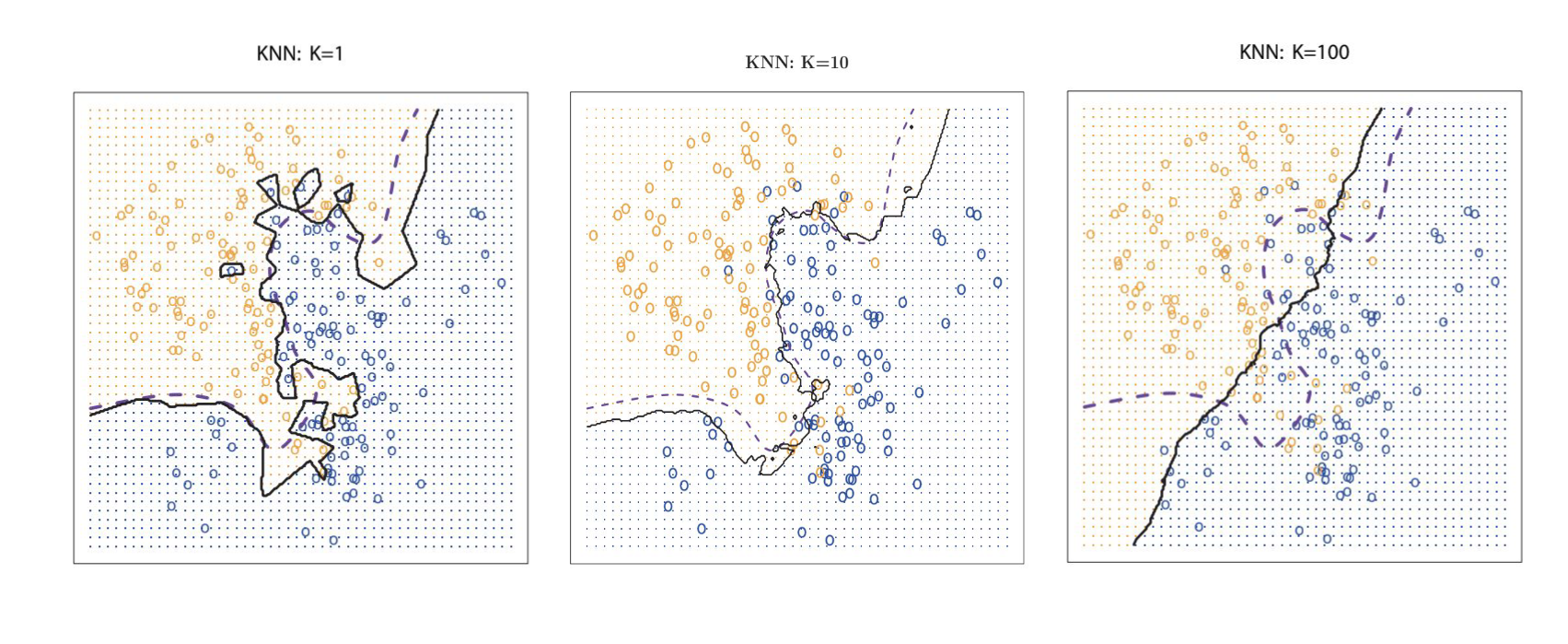
circles: training data
dashed line: decision boundary of data generating process
solid line: model
grid points: indicating which class is predicted in this are for new instances
Influence of K#
How would you interpret these models?
Influence of K#
K=1 → overfitting
K=10 → good fit
K=100 → underfitting

How do we determine the best value for K?#
test different numbers for K (e.g. with GridSearch)
→ take K with lowest error on validation data set

Distance Metrics#
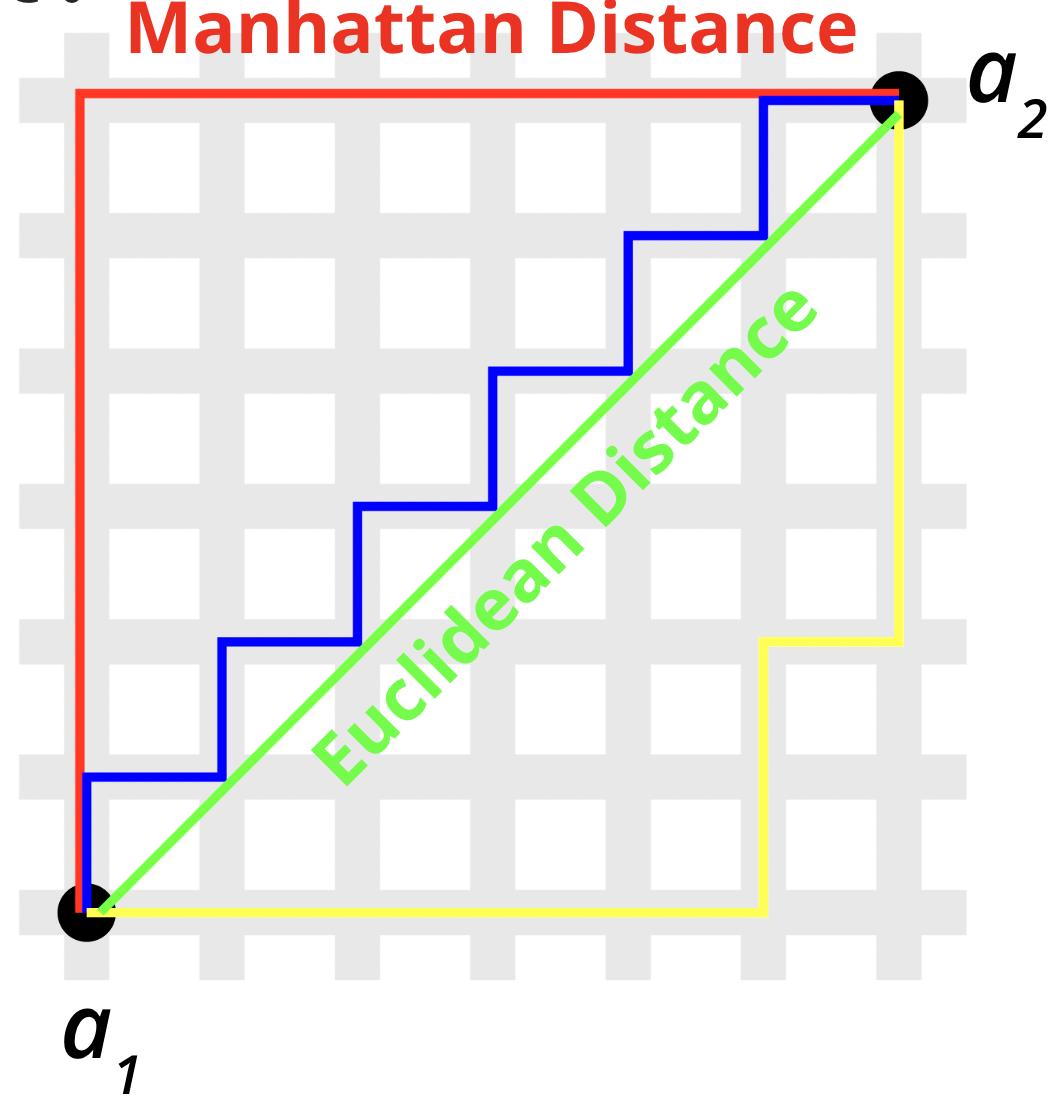
In this example the Euclidean Distance is used.
The Euclidean distance between two points (\(a_1\) and \(a_2\) ) is the length of the path connecting them.
\(\sqrt{\Sigma_{i=1}^{n}(a_{1,i} - a_{2,i})^2} = \sqrt{(a_{1,1} - a_{2,1})^2 + (a_{1,2} - a_{2,2})^2 } \)
where \(\textbf{n = number of feature}\)

What Distance Metrics exist?#
Euclidean Distance \(\sqrt{\Sigma_{i=1}^{n}(a_{1,i} - a_{2,i})^2}\)
Manhattan Distance \(\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|\)
sum of the absolute differences between the x-coordinates and y-coordinates
(Minkowski Distance \(\sqrt[p]{\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|^p}\))
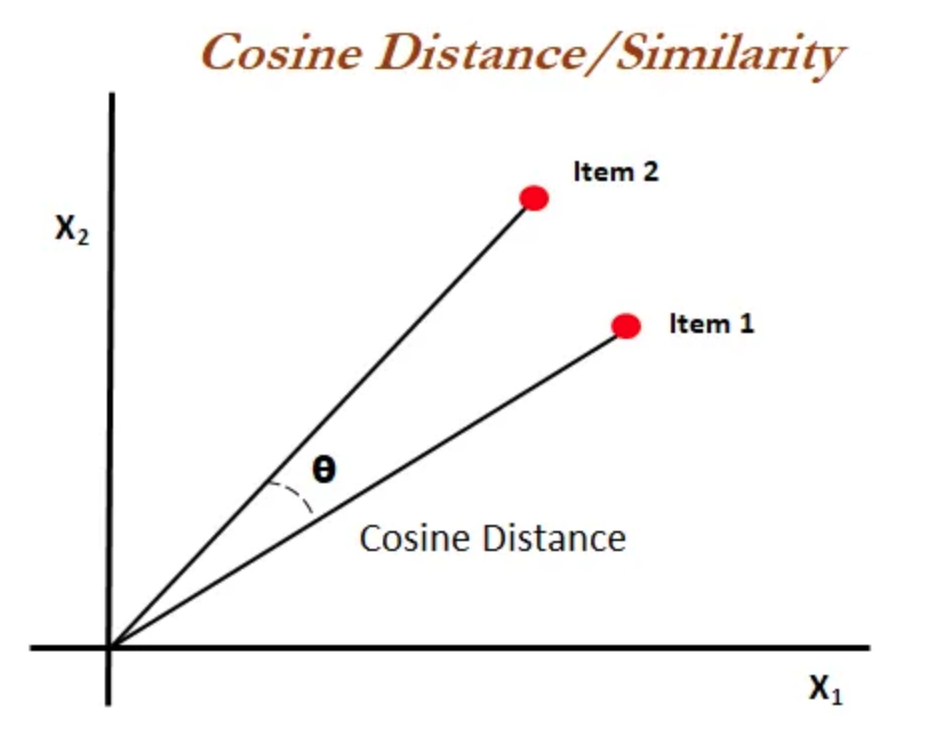
Cosine Distance#
COSINE SIMILARITY: the measure of similarity between two non-zero vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors.
Cosine Similarity: \( S_c(\vec A,\vec B)= cos(\Theta)= { \vec A \cdot \vec B} \div {|\vec A| |\vec B|} \)
COSINE DISTANCE = \( 1 - S_c(\vec A,\vec B) \)