Decision Trees

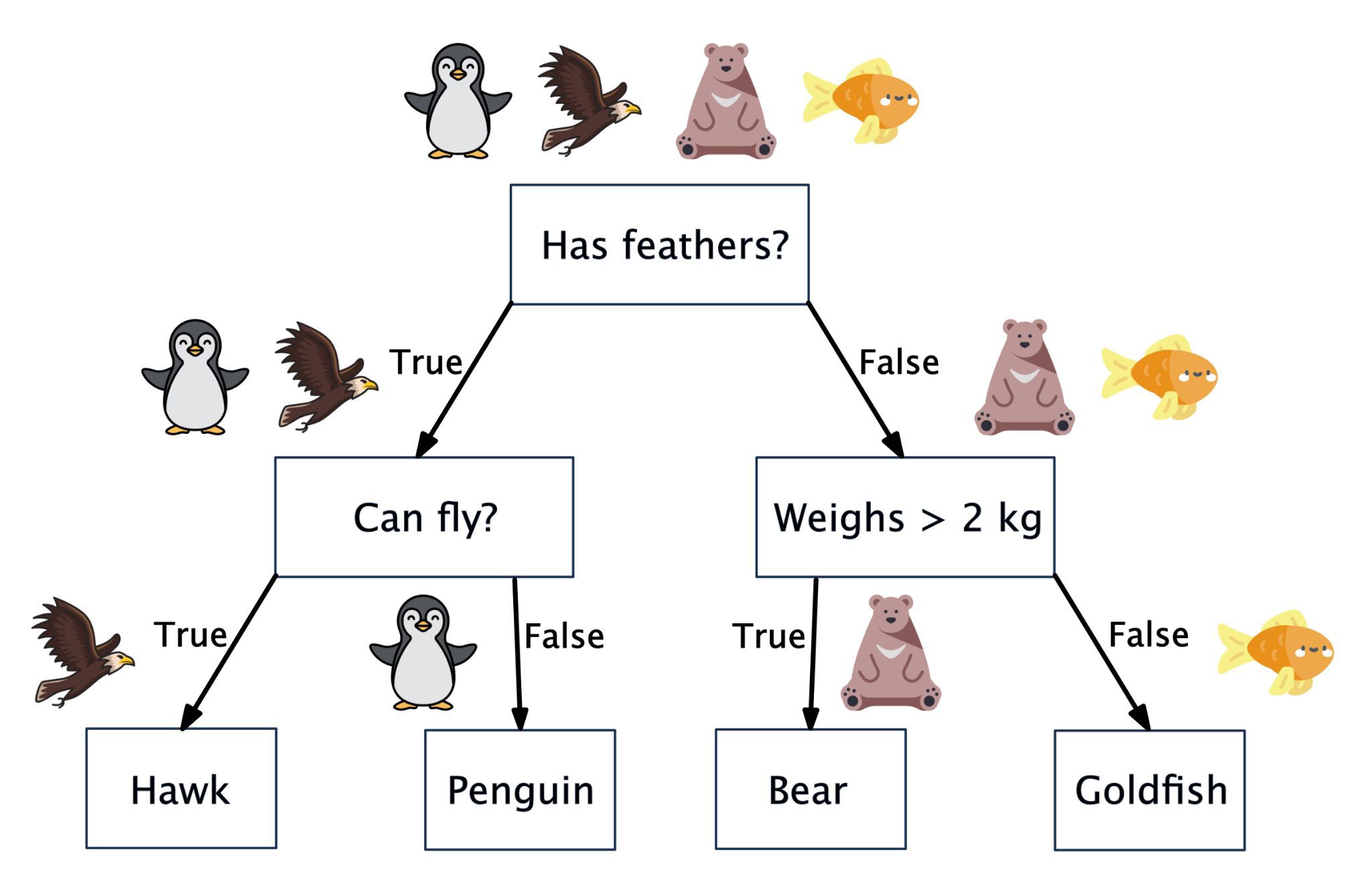
How would you differentiate these animals from one another?

(through their various features)

Notes:
Mention the purpose of DT first: Aim is to classify further animals of which you don’t know the label.
These animals (training dataset) have already been labeled/classified (penguin, hawk, …). Select whatever features enable you to classify new unknown animals.
Is this supervised/regression problem or what?

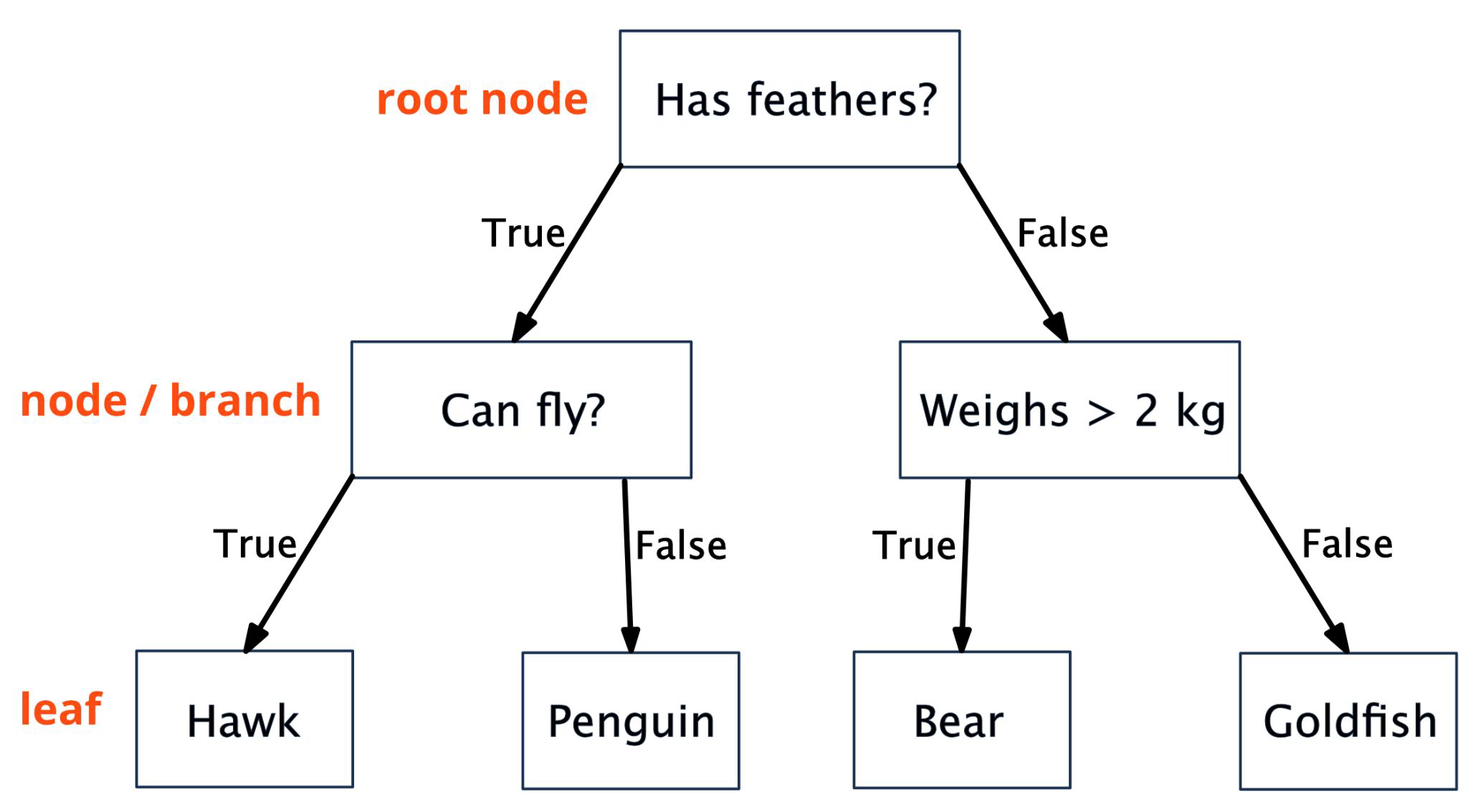
A Binary Tree

Decision trees are based on binary trees:

1 Question has 2 answers

= 1 Parent node has 2 children nodes

Notes:
A pigeon would be classified as a hawk. Why? Model is too simple.

A Binary Tree

First decision split is called root or root node

Each decision node compares a feature:

• True/False question (for categorical features)

• Larger than split (for numerical features)

Each leaf node (end node) represents a class label

To predict an unknown/new instance, we go through all the decisions in the tree until we end up at a leaf.

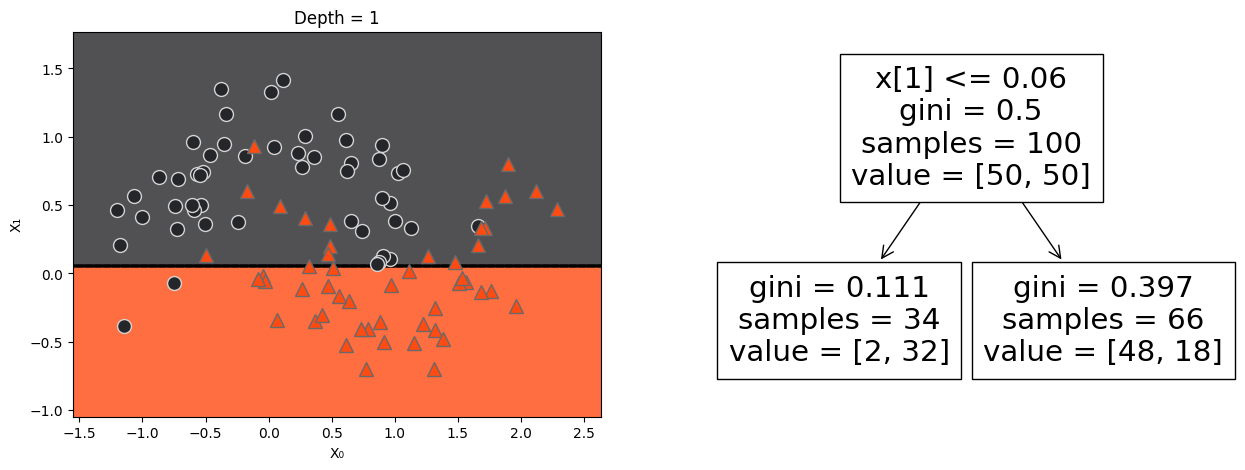
A Tree is built!

Node’s question - which feature and which threshold is appropriate - is chosen during training

This is done recursively until a stop condition is reached (e.g. less than 5 observations in a node, or node is pure).

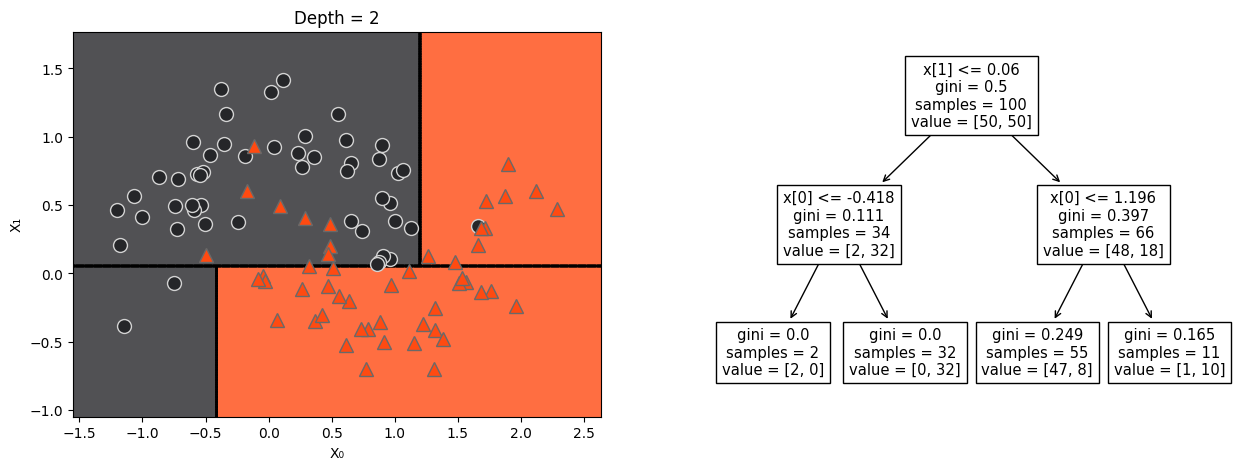
This is a tree with depth=2.

If the feature is continuous, decision work just as fine

1. The data are ordered in ascending order

2. Each mean between two adjacent data points is considered a splitting point

Notes:
This is funny: If 2 kg is the mean between the lightest bear and the heaviest goldfish …

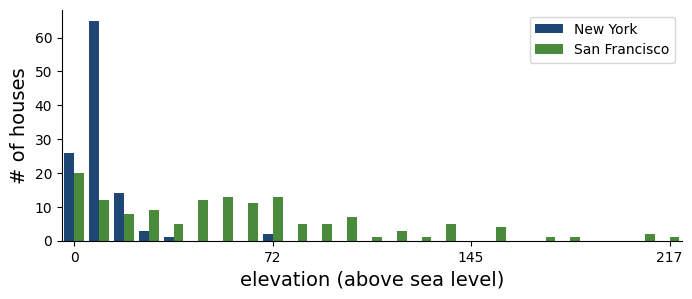
How to differentiate if a house is located in New York or San Francisco?

	bath	beds	elevation	price	price_per_sqft	sqft	target	year_built
0	1.0	2.0	10	999000	999	1000	0	1960

plot_elevation(housing_data)

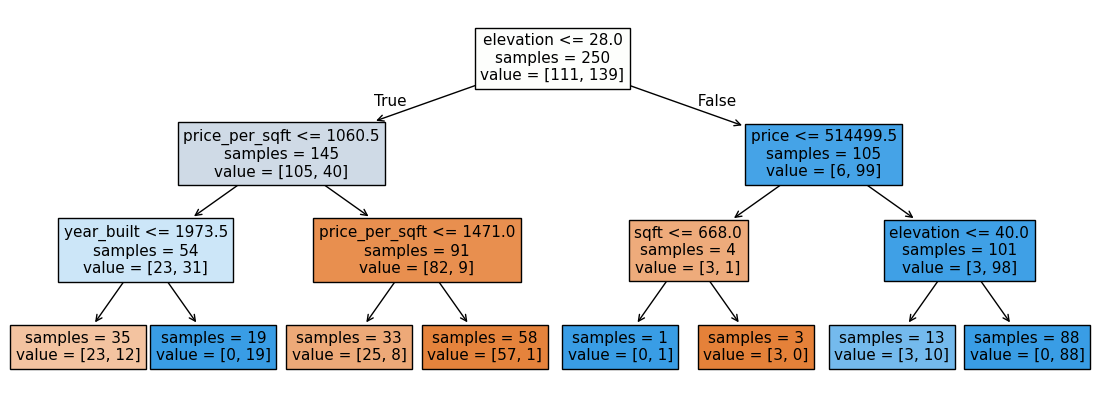
Interpreting Decision Tree

• First line of decision node: Feature name and split value

visual example

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[11], line 5
      2 clf_housing_max_depth_3 = DecisionTreeClassifier(max_depth=3, random_state=RSEED)
      3 clf_housing_max_depth_3.fit(X_housing, y_housing)
----> 5 plot_decision_tree(clf_housing_max_depth_3, X_housing, housing_colors, fig_size=(14, 5), fontsize=11, impurity=False)

Cell In[7], line 8, in plot_decision_tree(decision_tree, X, colors, fig_size, fontsize, impurity)
      6 r, g, b = to_rgb(colors[np.argmax(value)])
      7 f = impurity * 2 # for N colors: f = impurity * N/(N-1) if N>1 else 0
----> 8 artist.get_bbox_patch().set_facecolor((f + (1-f)*r, f + (1-f)*g, f + (1-f)*b))
      9 artist.get_bbox_patch().set_edgecolor('black')

AttributeError: 'NoneType' object has no attribute 'set_facecolor'

Interpreting Decision Tree

samples: How many observations are in the node
value: Target value distribution - Real number of observations per class

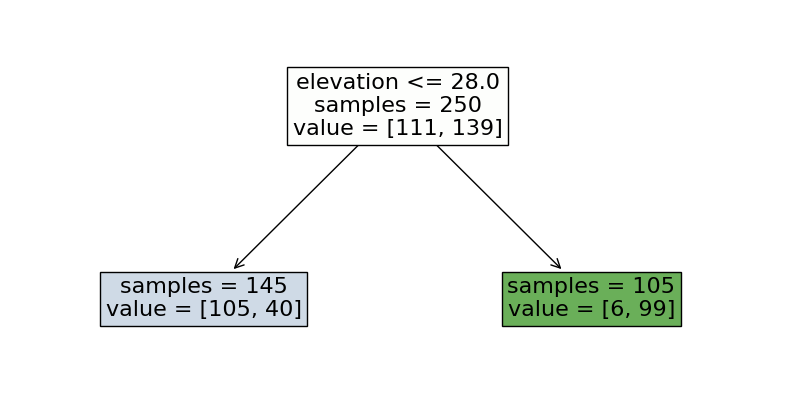
Interpreting Decision Tree

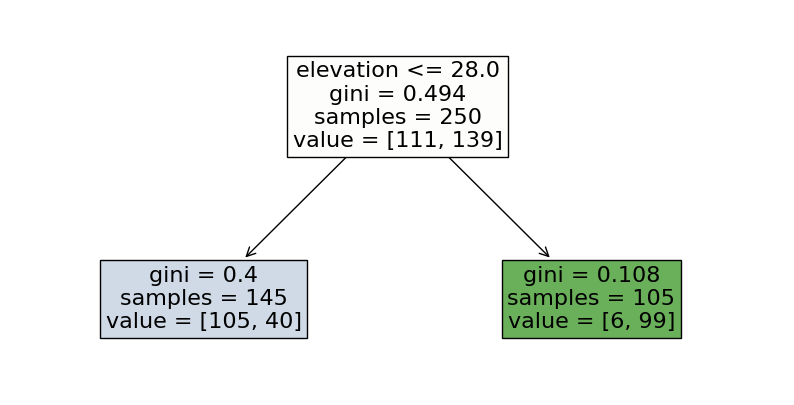
Is a house located in New York or San Francisco?

• Leaf node → prediction value

Interpreting Decision Tree

→ Confusion matrix based on one split

true \ pred	New York	San Francisco
New York	105	6
San Francisco	40	99

Interpreting Decision Tree

• Leaf node purity - leaf nodes where one class has an overwhelming majority are more reliable predictors

• Number of samples in leaf node: large leaf nodes are preferable, too few samples in leaves might be a sign of overfitting

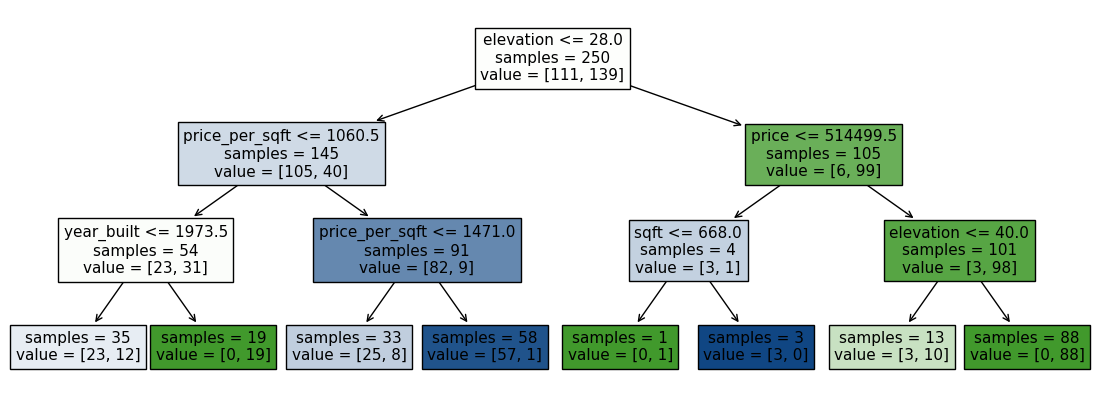
Why is it dangerous to grow a large tree?

Why is it dangerous to grow a large tree?

• Nodes will be splitted until leaves are pure

• Decision Trees can be extremely perceptive of the training data

• Tend to overfit the data

visual example

notes:

Decision trees are high-variance models. This means they can fit extremely complex patterns and noise in the training data if not constrained. When allowed to grow:

They split the data repeatedly, even for tiny differences.

Eventually, each leaf node may contain only one training example.

2. Overfitting Defined

Overfitting happens when a model performs very well on training data but poorly on unseen data. A deep decision tree can:

Learn anomalies or random fluctuations in the training data that don’t generalize.

Create very specific rules that don’t apply beyond the training set.

Decision Trees in a Nutshell

• Easy to interpret (white box)

• Can be used for regression and classification problems

• No feature scaling or centering needed

• No assumptions needed (e.g. linearity)

• Building block of Random Forests, Ada boost, Gradient boost

• Training is costly, prediction is cheap

• Tend to overfit the data

Splitting Decision

    Which feature to take first?

Which splitting point to choose?

Decision Trees can be based on different algorithms.

→ We will discuss Classification and Regression Trees (CART) by Breiman et al. (1984)

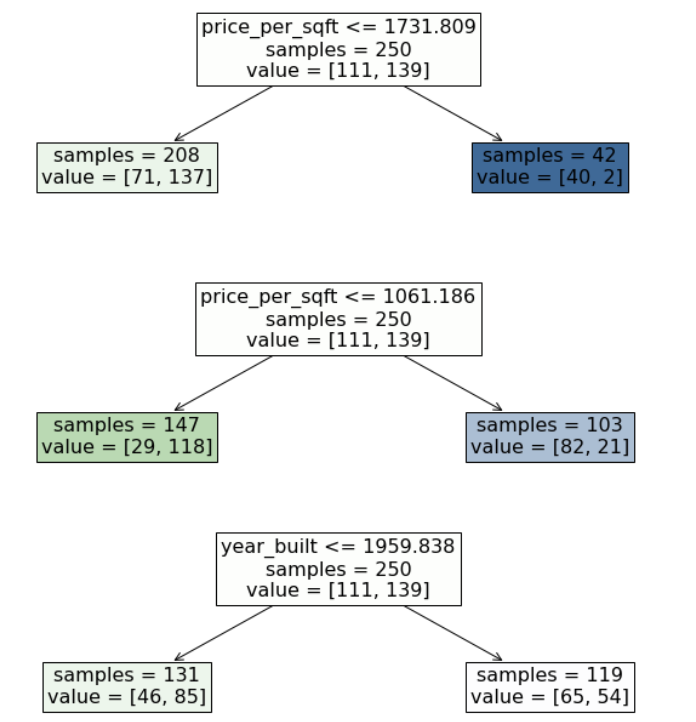
Which is the best split?

All leaves are impure, i.e. they do not devide the instances into a pure group.

Gini Impurity

In order to build a tree, we measure how pure the data split is.

On of the most common measures is the Gini impurity.

Alternatives are misclassification error or entropy.

Gini Impurity

• It tells you how often you would misclassify an item/observation if you guessed its class randomly using the class proportions in the group.

\[ I_{G}(p)\ =\ \sum_{i=1}^{J}\,p_{i}(1\ -\ p_{i})\ =\ 1-\sum_{i=1}^{J}\,p_{i}^{2}\]

Intuition of Gini Impurity

\[I_{G}(p)\ =\ \sum_{i=1}^{J}\,p_{i}(1\ -\ p_{i})\ =\ 1-\sum_{i=1}^{J}\,p_{i}^{2}\]

\[p_{green}(1-p_{green}) + p_{blue}(1-p_{blue})\]

\[I_{G}(p)=1-\color{#41992c}{\left(\frac{3}{10}\right)^2}-\color{#104683}{\left(\frac{7}{10}\right)^2}=0.42\]

Intuition of Gini Impurity

\[\begin{split}\begin{align} I_{G}(p)&=1-\color{#41992c}{\left(\frac{0}{10}\right)^2}-\color{#104683}{\left(\frac{10}{10}\right)^2}=0.0 \\ I_{G}(p)&=1-\color{#41992c}{\left(\frac{3}{10}\right)^2}-\color{#104683}{\left(\frac{7}{10}\right)^2}=0.42 \end{align}\end{split}\]

\[\begin{split}\begin{align} I_{G}(p)&=1-\color{#41992c}{\left(\frac{10}{10}\right)^2}-\color{#104683}{\left(\frac{0}{10}\right)^2}=0.0 \\ I_{G}(p)&=1-\color{#41992c}{\left(\frac{7}{10}\right)^2}-\color{#104683}{\left(\frac{3}{10}\right)^2}=0.42 \end{align}\end{split}\]

\[I_{G}(p)=1-\color{#41992c}{\left(\frac{5}{10}\right)^2}-\color{#104683}{\left(\frac{5}{10}\right)^2}=0.5\]

1. Gini impurity for each node

\[ 1\,-\,\left(\frac{111}{250}\right)^{2}-\left(\frac{139}{250}\right)^{2}=\,0.494\]

\[\begin{split}\begin{align} 1-\left(\frac{105}{145}\right)^{2}-\left(\frac{40}{145}\right)^{2}\,&=\,0.4 \\ 1-\left(\frac{6}{105}\right)^{2}-\left(\frac{99}{105}\right)^{2}\,&=\,0.108 \end{align}\end{split}\]

2. How well does the split perform overall?

Just calculate the average of the impurities of the leaves, of course weighted by their impact (= rel. number of obs.):

\[ 0.4\ \cdot{\frac{145}{250}}+\ 0.108\ \cdot{\frac{105}{250}}=\;0.277\]

Which is the best split?

Let's calculate the Gini impurity for each possible split.

\( I_{G}(p)\ =\ \sum_{i=1}^{J}\,p_{i}(1\ -\ p_{i})\ =\ 1-\sum_{i=1}^{J}\,p_{i}^{2}\)

Gini impurity of the split is the weighted average of the impurities of the leaves.

Finally, the best splitting point is the one, which minimizes the Gini Impurity of the split.

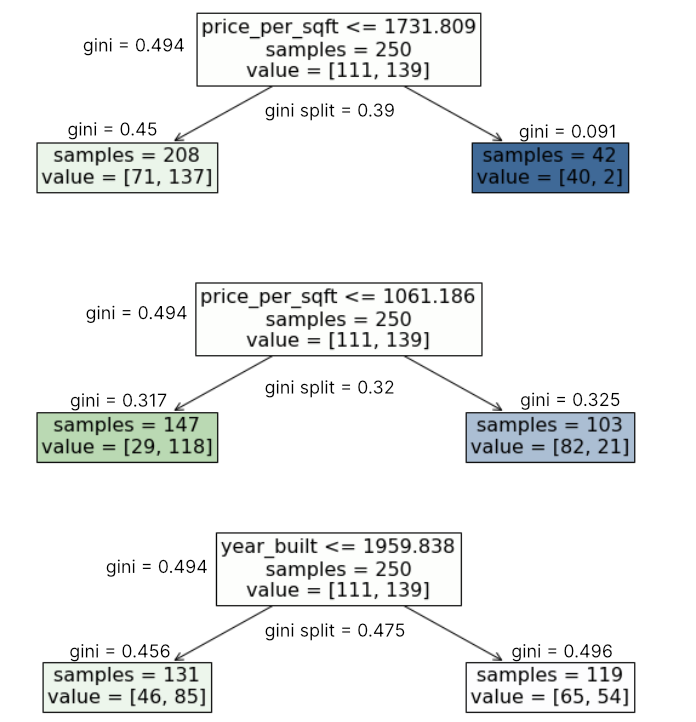
Tree build with two continous features

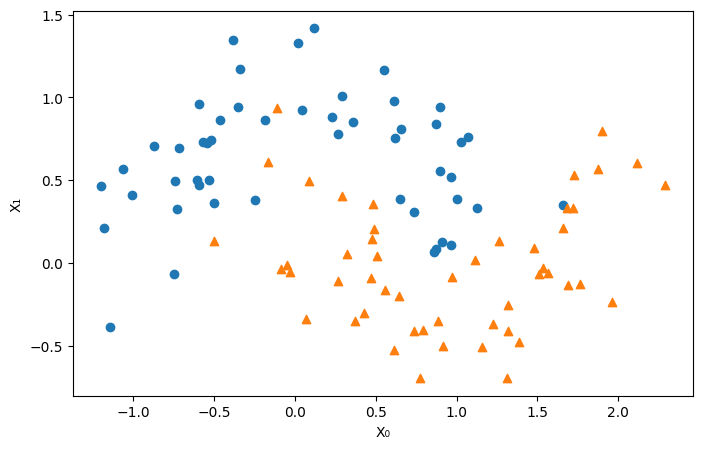
Tree build with two continous features

The second split

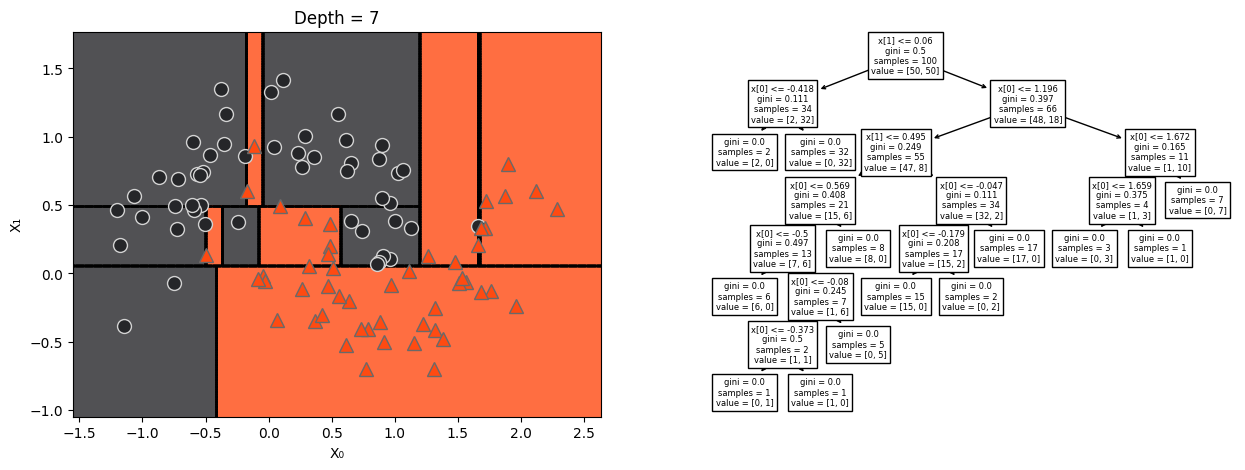
Growing a full tree

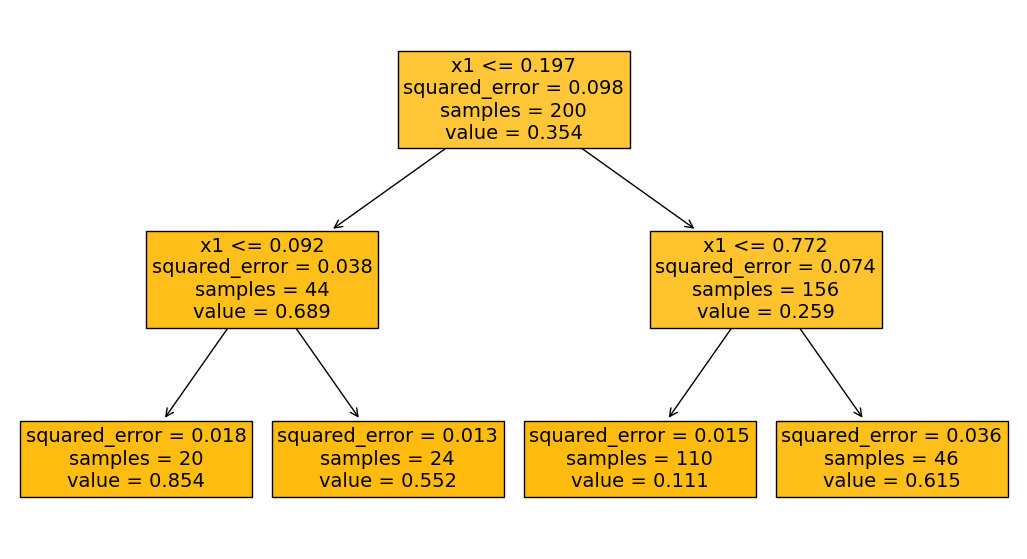
Regression Trees

• Similar approach as with classification trees, but split data based on MSE not impurity

• Traverse tree to get predicitons for new instance, which is mean of target values of all observations in one leaf

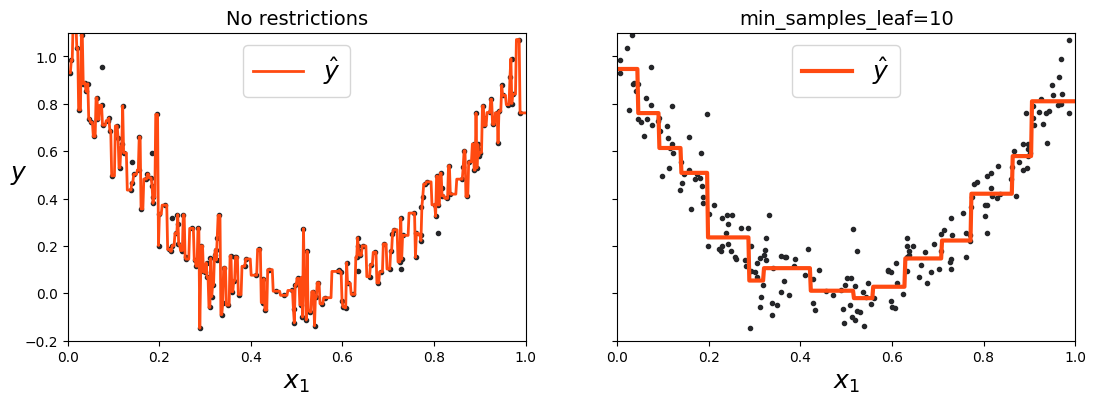
Regularisation is needed!

Regularisation

Decision Trees will recursively split the data until nodes are pure no matter how small the sample size will be.

→ High chance of overfitting.

Solution:

Pruning Trees → limiting the number of branches/leaves

Pruning Trees - max_leaf_nodes

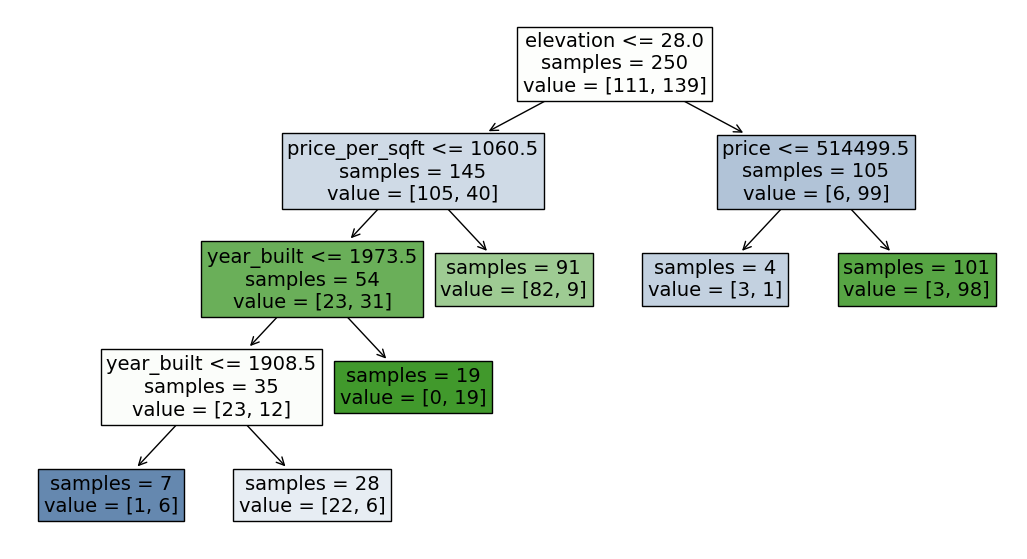
Pruning Trees - max_depth

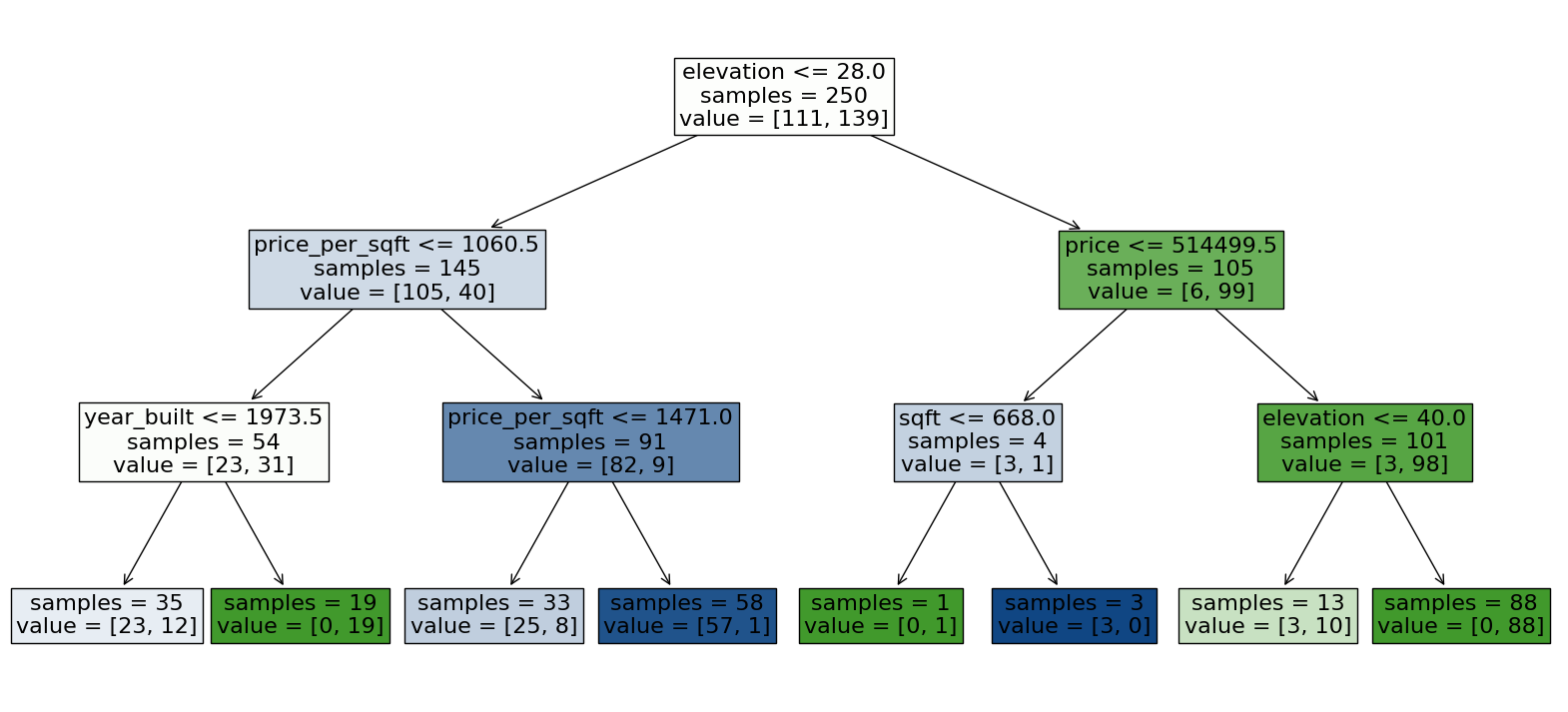
Pruning Trees - min_samples_split

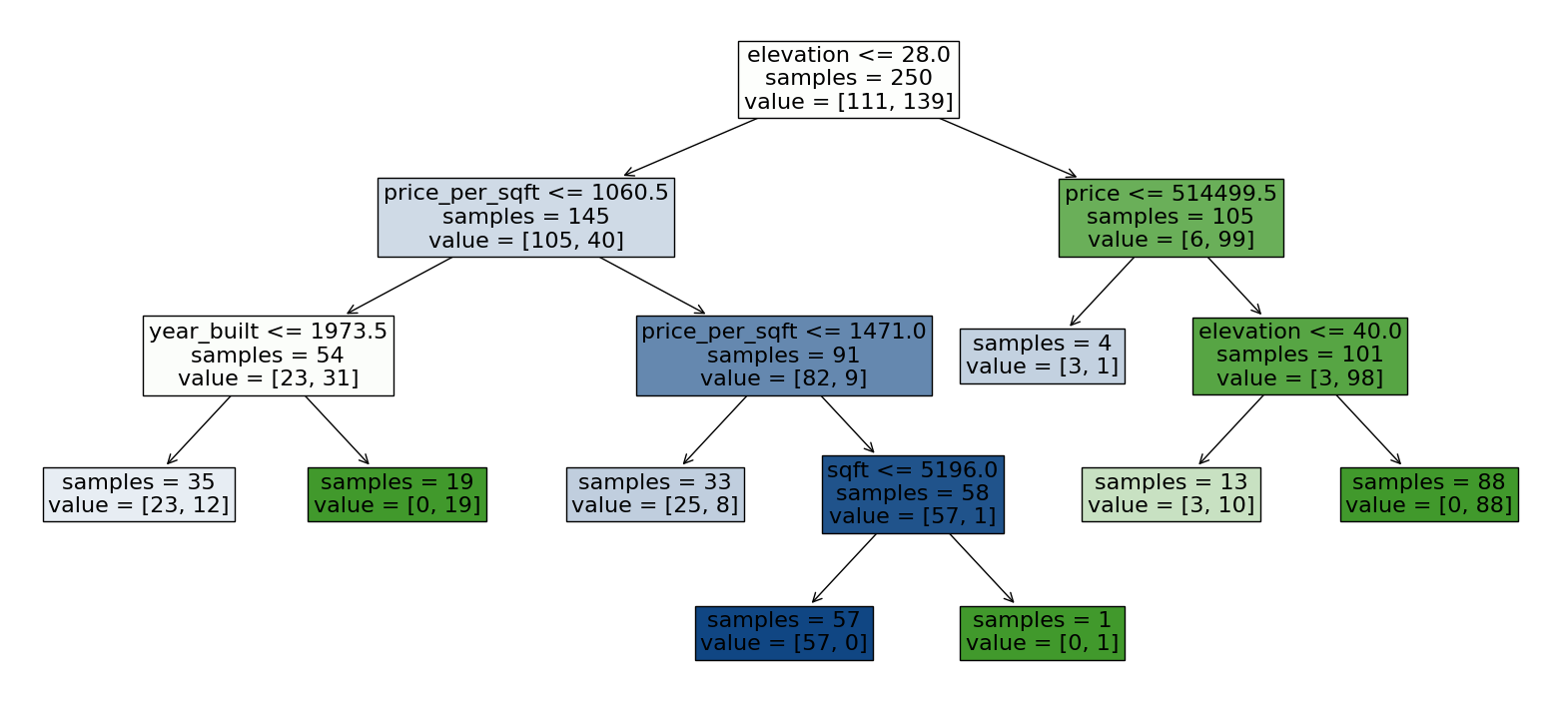
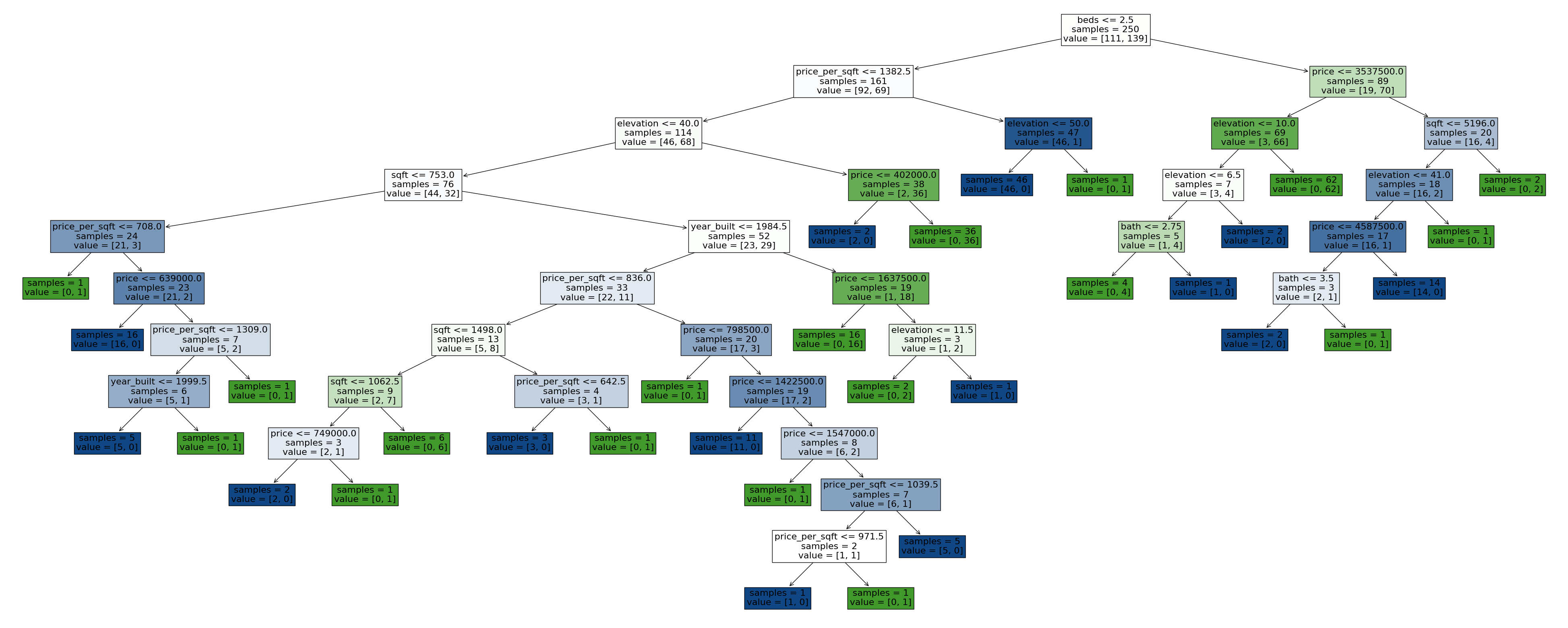
Pruning Trees - max_features

References

Code for plots:

Hands on ML repo, A. Geron

Introduction to Machine Learning with Python repo, A. Müller and S. Guido